Elmecha
1. óra Letöltés
Hatáselvek
Az óra célja röviden az, hogy megismerkedjünk a variációs módszerekkel. Ez gyakorlatilag egy új nyelv, amire az eddig megszokotthoz (rajzolni egy diagramot az erőkkel, aztán $\vec{F}=m\vec{a} $) hasonlóan le lehet fordítani azt, hogy mi történik a világban. Az előnye az, hogy általában sokkal könnyebb felírni így a mozgást leíró egyenleteket, mégha megoldani nem is mindig lehet azokat. Mellékesen pedig ezen a nyelven lesz olvasható a későbbiekben két egész fontos ága a tudományunknak: a kvantumfizika és az általános relativitáselmélet.
Mechanikáról léve szó, azt szeretnénk megtudni, hogy hogyan jutunk el valamilyen $A$ pontból a $B$-be. Ezt sokféle úton lehetne megtenni, sok féle $\Gamma$ görbén; amik mentén változhat a "fizika" valamilyen (egyelőre) ismeretlen $f$ függvények által kódolva. A függvények és a görbék relatíve bonyolult dolgok, ezért keressünk valami egyszerűbbet, mondjuk egy számot amit hívjunk $\mathcal{S}$-nek. Hogy ez is kódolja az összes eddigi információt, legyen absztraktul $$ \mathcal{S} = \mathcal{S}[f(\Gamma)] $$ Ami nevesítve azt mondja, hogy $\mathcal{S}$ egy funkcionál: ahogyan egy $f$ függvény (function) egy számhoz hozzárendel egy másikat, az $\mathcal{S}$ funkcionál egy függvényhez rendel hozzá egy számot.
A fizika ott kezdődik, hogy eközül a sok út közül csak egy lehet reális: az alma nem keringőzik a levegőben, hanem leesik. Kitüntetett szerepe annak az útnak lesz, ahol ez az $\mathcal{S}$ hatás alig változik: extrémuma van. A legkisebb hatás elve szerint tehát az lesz a fizikailag megvalósuló pálya, amelynek mentén $$ \delta \mathcal{S} = 0 $$

Korai minimumelvek
A kérdés már csak az, hogy mi is ez az $\mathcal{S}$ hatás. Először néhány történelmi példával kezdünk, és megbarátkozunk a minimalizálásával. Az előadáson hallhattunk két fontos elvet: $$ \begin{aligned} \mathcal{S}_0 = \int |\vec{p}| \rd s \quad\quad \mathcal{T} = \int n(s) \rd s \end{aligned} $$ amikről beláthattuk, hogy azonosan viselkednek. A Fermat elvet már ismeritek, és levezettétek belőle a Snellius-Descartes törvényt, miszerint fénytörés esetén a beesési szögek és a törésmutatók közti összefüggés: $$ \begin{aligned} n_1 \sin{\varphi_1} = n_2 \sin{\varphi_2} \end{aligned} $$ A Maupertuis elv még új, szóval első példáinkban barátkozzunk vele egy kicsit.
1.1 példa: Úttörés részecskére
Van egy tömegpontunk (mondjuk egy elektron) ami kezdetben szabadon mozog egyenes vonalban, egyenletes sebességgel. Az $x$ tengelyt elérve viszont azt tapasztalja, hogy lecsökken a potenciális energiája: a negatív tartományban a fentihez képest egy konstans $-U$ potenciál tölti ki a teret.
1.1.1. Mi történik a részecske pályájával?
Ezt a feladatot kicsit macerás megoldani a Newton törvényekkel, szóval azt későbbre hagyjuk. Használjuk helyette a Maupertuis elvet, illetve az energiamegmaradást, felírva a tengelyen áthaladás előtti és utáni pillanatokra: $$ \begin{aligned} K_1 &= K_2 - U \\ \frac{1}{2}m v_1^2 &= \frac{1}{2}m v_2^2 - U \\ \frac{p_1^2}{2m} &= \frac{p_2^2}{2m} - U \\ p_1^2 &= p_2^2 - 2mU \\ |\vec{p}_2| &= \sqrt{p_1^2 + 2mU} \end{aligned} $$ A pontos alak most annyira nem is fontos, a lényeg az, hogy ez konstans fent is és lent is (még ha nem is ugyanaz a konstans).
A hatás felírásához szükség lesz még a megtett utakra, amiket valahogy paraméterezni kell egy koordinátarendszerben. Legyen az Origó a kiindulási $P_1$ pont $x$ tengelyre vetett képe, a tengelyen áthaladás pontját pedig vegyük fel valamilyen $x$ pontban, amire végső soron kíváncsiak vagyunk. Két szöget is be tudunk rajzolni, ezek mindjárt hasznosak is lesznek.
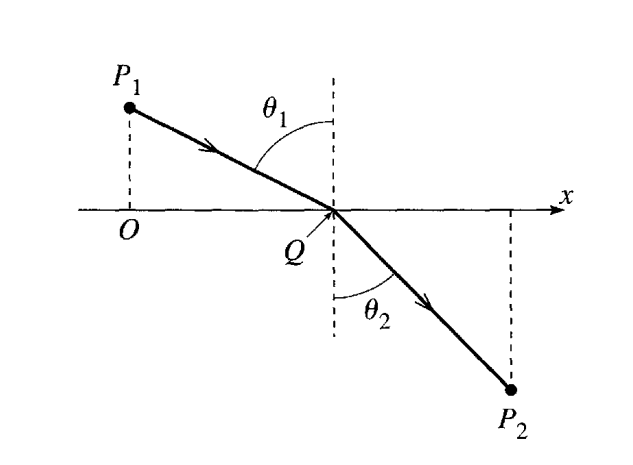
A hatásunk egy út szerinti integrál: bontsuk fel ketté. $$ \begin{aligned} \mathcal{S}_0 = \int_{P_1}^{P_2} |\vec{p}(s)| \rd s = \int_{P_1}^{Q} |\vec{p}_1| \rd s + \int_{Q}^{P_2}|\vec{p}_2| \rd s \end{aligned} $$ Mivel az impulzusok már konstansok, így ami marad az magának az útnak a kiintegrálása. Mivel ez két egyenes hossza, ez egészen egyszerű: $$ \begin{aligned} \mathcal{S}_0 = p_1 \sqrt{x^2 + y_1^2} + p_2 \sqrt{(x_2-x)^2+y_2^2} \end{aligned} $$ A Maupertuis elv szerint ez minimális kell, hogy legyen. Nekünk $x$ az egyetlen dolog ami változhat, tehát $$ \begin{aligned} \frac{\partial \mathcal{S}_0}{\partial x} &= 0 \\ p_1 \frac{x}{\sqrt{x^2 + y_1^2}} -p_2 \frac{x_2-x}{\sqrt{(x_2-x)^2+y_2^2}} &= 0 \end{aligned} $$ Kis trigonometriával $$ \begin{aligned} \sin{\theta_1} = \frac{x}{\sqrt{x^2 + y_1^2}} \quad\quad \sin{\theta_2} = \frac{x_2 - x}{ \sqrt{(x_2-x)^2 + y_2^2}} \end{aligned} $$ tehát $$ \begin{aligned} \boxed{p_1 \sin{\theta_1} = p_2 \sin{\theta_2}} \end{aligned} $$
Ezzel meg is oldottuk a feladatot: a potenciális energia ugrása pont olyan hatással van a részecskére, mint a törésmutató ugrása a fényre. Ha magukat a sebességeket nem ismerjük, csak a potenciált és a kimenő sebességet (ami gyakori, ha például egy laborban mi magunk rakjuk oda a potenciális energiát, és detektáljuk a kijövő részecskét), akkor átírva: $$ \begin{aligned} \frac{\sin{\theta_1}}{\sin{\theta_2}} = \sqrt{1 + \frac{2m}{p_1^2} U} \end{aligned} $$
1.1.2. Hová lett a lendületmegmaradás?
Már az energiamegmaradás első felírt sorában láthattuk, hogy a lendület itt gyanúsan nem marad meg. Hogy ezt kicsit jobban kivesézzük, bontsuk fel a lendületeket komponensekre $\vec{p} = (p_x, p_y)$ módon, és nézzük meg az $x$ irányúakat: $$ \begin{aligned} p_{1,x} = |\vec{p_1}|\sin{\theta_1} \quad\quad p_{2,x} = |\vec{p_2}|\sin{\theta_2} \end{aligned} $$ Rögtön láthatjuk: $$ \begin{aligned} p_{1,x} = p_{2,x} \end{aligned} $$ tehát a határfelülettel párhuzamos irányú lendület nem változik, megmarad. Ennek mélyebb oka a szimmetriákban rejlik: a rendszerünk szimmetrikus arra, hogy eltoljuk a $P_1$ és $P_2$ pontokat a tengellyel párhuzamosan, attól nem változik semmi. Ha arra merőlegesen tolnánk el, akkor viszont beleütközhetünk a falba, amin túl már nem ugyanarról a fizikai problémáról beszélünk.
1.1.3. Newtonos megoldás
A feladat régimódibb megoldásához kis trükközésre van szükség. Végső célunk megoldani a Newton-egyenletet, ami az energiamegmaradásnak hála $$ \begin{aligned} -\nabla U = \dot{\vec{p}} \end{aligned} $$ Ami itt bajos lehet, az a $\nabla U$. Nekünk ez a lépcsőszerű ugrás a potenciálban a Heaviside lépcsőfüggvénnyel írható le $$ \begin{aligned} U(x,y) = -U \Theta(-y) \end{aligned} $$ Ami nem folytonos, ezért deriválni sem lehet szépen disztribúcióelmélet nélkül. Ha éppen nem jut eszünkbe, hogy az alapján ennek pont egy Dirac-delta a deriváltja, akkor a következő trükköket lehet bevetni.
A lépcsőfüggvény sokféleképpen közelíthető. Egyik mód például a $$ \begin{aligned} \Theta(y) \approx \frac{1}{2} + \frac{1}{2} \tanh{(ky)} \end{aligned} $$ ami visszaadja a lépcsőt, ha $k\rightarrow \infty$. Ezt már vígan lehet deriválni: $$ \begin{aligned} \partial_y \Theta(y) \approx \frac{1}{2}\frac{k}{\cosh^2{(ky)}} \end{aligned} $$ Ennek a függvénynek pedig van egy hasznos tulajdonsága: $$ \begin{aligned} \int_{-\infty}^\infty \frac{1}{2}\frac{1}{\cosh^2{u}} \rd u = 1 \end{aligned} $$ Beírva, a Newton törvény alakja: $$ \begin{aligned} U \begin{pmatrix} 0 \\ \frac{1}{2}\frac{k}{\cosh^2{(ky)}} \end{pmatrix} = \frac{\rd}{\rd t} \begin{pmatrix} p_x \\ p_y \end{pmatrix} \end{aligned} $$ Amiből rögtön látszik, hogy $p_x$ állandó. A másik komponensre vonatkozó egyenlet pedig $$ \begin{aligned} U \frac{1}{2}\frac{k}{\cosh^2{(ky)}} = \frac{\rd p_y}{\rd t} \end{aligned} $$ Ha ennek a kezdeti és végállapotbeli megváltozására vagyunk kíváncsiak, akkor egy kis $$ \begin{aligned} \frac{\rd p_y}{\rd t} \rd y = \frac{\rd y }{\rd t}\rd p_y = \dot{y} \rd p_y = \frac{1}{m} p_y \rd p_y \end{aligned} $$ átírás után kiintegrálhatjuk az egyenlet mindkét oldalát $y$ szerint: $$ \begin{aligned} U \int \frac{1}{2}\frac{k}{\cosh^2{(ky)}} \rd y &= \frac{1}{m} \int p_y \rd p_y \\ U &= \frac{1}{2m} \Delta p_y^2 \end{aligned} $$ Tehát tisztán $y$ irányban kapott a kis részecskénk egy impulzuslöketet.
1.2 példa: Legnagyobb (?) hatás elve
Nézzünk egy példát a fényre is. A Fermat elv szerint a fény a legrövidebb időbe kerülő úton közlekedik, tehát az a pálya valósul meg, amelynek mentén a megtett idő minimális. $$ \begin{aligned} \mathcal{T} = \int n(s) \rd s \end{aligned} $$ Most bebizonyítjuk, hogy ez így nem igaz, egy görbe tükör segítségével.
Vegyük az kezdeti $A$ és a végződő $B$ pontokat egy félgömb alakú tükör két végében. Természetesen a legrövidebb út köztük az egyenes, de optikából tudjuk, hogy a fény tud másmerre is menni: tükröződve. Vegyük fel valahol a köztes $P$ pontunkat a köríven, és paraméterezzük az ábrán látható szöggel.
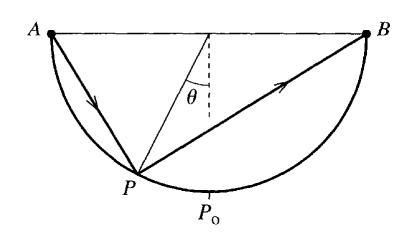
Kis geometria után (Egyenlő $R$ szárú háromszögeink vannak, amiket meg tudunk felezni. A szárszöget a $\theta$ paraméterünkből és a 90 fokból tudjuk kikombinálni, ami után egy szinusz felismerése a feladat.) a megtett útszakaszok: $$ \begin{aligned} \overline{AP} = a = 2 R \sin{\left( \frac{\pi/2 - \theta}{2}\right)} \quad\quad \overline{PB} = b = 2 R \sin{\left( \frac{\pi/2 + \theta}{2}\right)} \end{aligned} $$ A Fermat-elvhez fordulva a legrövidebb időre törekszünk. De itt most a törésmutató éppen konstans, tehát ez ekvivalens lesz a legrövidebb úttal, azaz $$ \begin{aligned} \mathcal{T} \cdot \frac{c}{n} = \mathcal{S} = 2R \left[\sin{\left( \frac{\pi/2 - \theta}{2}\right)} + \sin{\left( \frac{\pi/2 + \theta}{2}\right)} \right] \end{aligned} $$ Ezt kell most deriválnunk $\theta$ szerint, majd nullává tennünk. $$ \begin{aligned} \partial_\theta \mathcal{S} = -R\cos{\left( \frac{\pi/2 - \theta}{2}\right)} &+ R\cos{\left( \frac{\pi/2 + \theta}{2}\right)} = 0 \\ \cos{\left( \frac{\pi/2 - \theta}{2}\right)} &= \cos{\left( \frac{\pi/2 + \theta}{2}\right)} \end{aligned} $$ Őt megoldhatjuk vizuálisan is, esetszétválasztással, vagy felhasználhatunk egy koszinuszok különbségére vonatkozó összefüggést, aminek hála $$ \begin{aligned} \sin{\frac{\theta}{2}} = 0 \end{aligned} $$
Minden esetre a megoldásaink: $$ \begin{aligned} \theta = 2n \pi \,, \hspace{10mm} n\in \mathbb{Z} \end{aligned} $$ Nekünk ezek közül $\theta=0$ lesz az fontos, minden más ugyanazt jelenti.
Érdekes dolgot figyelhetünk meg viszont, ha megnézzük az időtartam második deriváltját is a minimumban. $$ \begin{aligned} \left. \partial_\theta^2 \mathcal{T} \right|_{\theta=0} \propto -R \left[\sin{\frac{\pi}{4}} +\sin{\frac{\pi}{4}} \right] \\ \propto -R \sin{\frac{\pi}{4}} \end{aligned} $$ Ami negatív. Visszaidézve a korábbi matekos tudásunkat, ez azt jelenti, hogy a megvalósuló pályánk nem is egy minimumhoz köthető. Pont ellenkezőleg, egy lokális maximumhoz tartozó pályát követ ezesetben a fény.
Éppen ezért, most is és a jövőben is, bármikor, ha a legkisebb hatás elvét emlegeti valaki, akkor az általában csak egy megszokott elnevezés. Valójában inkább a szélsőértékes hatás elvére gondolunk, de az sokkal csúnyábban hangzik mind magyarul, mind angolul. (A pontosságra törekedőknek a stacionárius a bevett szó.)
Feltűnhetett, hogy mindkét példában az integrálás igazból egy-egy egyenes hosszának kiszámolására redukálódott. Ez csak didaktikus, és mutatja a Maupertuis elv hátrányát: mást nem igazán tudtunk volna kiszámolni. A probléma az integrálással van, hiszen azt nem mindig lehet elvégezni; és itt az integrálás után szelektáljuk ki az összes lehetséges útból az igazit. Ha kegyes a fizika, akkor létezik olyan módszer, ami ezeket megcseréli.
A Lagrange formalizmus
Felidézve, hogy a hatástól megköveteljük, hogy stacionárius legyen: $$ \begin{aligned} \delta \mathcal{S} = 0 \end{aligned} $$ Vegyünk rá most egy általánosabb alakot az eddigieknél. Legyen $$ \begin{aligned} \mathcal{S} = \int_A^B \mathcal{L}\Bigl(x(t), \dot{x}(t),t \Bigr) \rd t \end{aligned} $$ Hogy ez minimális legyen, alkalmazzuk a funkcionál deriválás szabályait: kapunk egy szép egyenletet az $\mathcal{L}$ Lagrange-függvényünkre: $$ \begin{aligned} \frac{\rd}{\rd t} \frac{\partial \mathcal{L}}{\partial \dot{x}} = \frac{\partial \mathcal{L}}{\partial x} \end{aligned} $$ az úgy nevezett Euler-Lagrange-egyenletet. Ez egyelőre még lehet, hogy csúnyábbnak tűnik mint az $\vec{F} = m \vec{a}$, de pont arra van a gyakorlat, hogy megbarátkozzunk vele. Úgy általánosságban két féle példával fogunk találkozni: lesznek a tipikus feladatok, ahol ezt kell használni ahogy van; és lesznek gondolkodósak, ahol ezt az egyenletet nem lehet csak úgy ráküldeni a problémára. Nézzünk először pár példát az utóbbira.
1.3 példa: Eukleidész
Az első kérdés amit segít megválaszolni a variációszámítás a következő:
Mi a legrövidebb út két pont között?
1.3.1 Paraméterezés
Próbáljunk meg elvonatkoztatni attól, hogy tudjuk a választ (egyenes). Ha ez megvolt, akkor rajzoljunk le valami általános görbét $A$ és $B$ pontok közt, ahogy azt az ábrán láthatjuk. Végső soron arra leszünk kíváncsiak, hogy ennek a görbének a hossza mikor lesz minimális: tehát számunkra ő most az $\mathcal{S}$ hatás. Hogy őt megkapjuk egy integrállal, a görbe mentén kell felösszegeznünk a kis $\rd s$ ívelemeket, tehát $$ \begin{aligned} \mathcal{S} = \int_A^B \rd s \end{aligned} $$
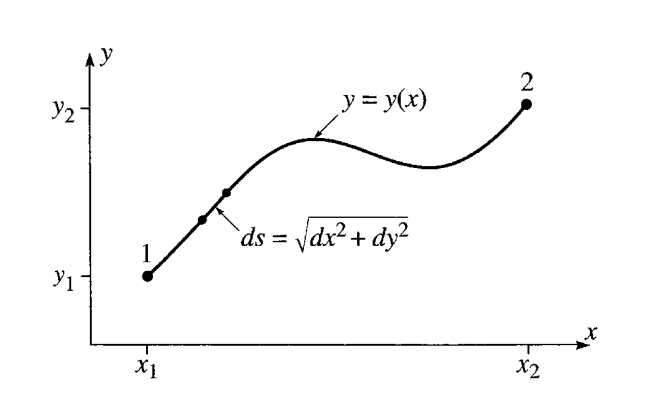
Amivel meg is van a feladat filozofálósabb része. Ami marad az az, hogy hogyan kell ezt az integrálást elvégezni: mik is a határok, és hogy függ tőlük az ívelem. Descartes-i koordinátákban dolgozva általánosan is igaz, hogy két pont közt a távolság $s^2 = x^2 + y^2$. Ez alapján az infinitezimális elmozdulásokra is valid lesz: $$ \begin{aligned} \rd s = \sqrt{\rd x^2 + \rd y^2} \end{aligned} $$ Ami már majdnem jó, de nekünk csak $x$ a változó, amitől függ maga az $y$, ezért azt a $\rd y$-t el lehet tűntetni. Szorozzuk be eggyel: $$ \begin{aligned} \rd y = \rd y \frac{\rd x}{\rd x} = \frac{\rd y}{\rd x} \rd x = y^\prime(x) \rd x \end{aligned} $$ Ezzel a hatásintegrálunkat már fel tudjuk írni mint egy szokásos, $x$ szerinti integrálás: $$ \begin{aligned} \mathcal{S} = \int_{x_A}^{x_B} \sqrt{\rd x^2 + y^{\prime 2}(x) \rd x^2} = \int_{x_A}^{x_B} \sqrt{1 + y^{\prime 2}(x) } \rd x \end{aligned} $$
1.3.2 Variáció
Megtaláltuk tehát, hogy mi az a Lagrange-függvény ami ezt a problémát írja le: $$ \begin{aligned} \mathcal{L}(y(x), y^\prime(x)) = \sqrt{1 + y^{\prime 2}(x) } \end{aligned} $$ Ennek véve a deriváltjait: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial y} = 0 && \frac{\partial \mathcal{L}}{\partial y^\prime} = \frac{1}{2}\frac{2 y^\prime}{\sqrt{1+y^{\prime 2}}} \end{aligned} $$ Aztán felírhatjuk persze az Euler-Lagrange egyenletet, amihez kell még ez utóbbinak a teljes deriváltja. Most ez ki fog derülni, hogy felesleges, de gyakorlásként nézzük meg. $$ \begin{aligned} \frac{\rd}{\rd x}\frac{\partial \mathcal{L}}{\partial y^\prime} &= \frac{y^{\prime\prime} \times \sqrt{1+y^{\prime 2}} - y^\prime \times \frac{y^\prime y^{\prime\prime}}{\sqrt{1+y^{\prime 2}}}}{1+y^{\prime 2}} = 0 = \frac{\partial \mathcal{L}}{\partial y} \\ &= y^{\prime\prime}\frac{\sqrt{1+y^{\prime 2}} - \frac{y^{\prime 2}}{\sqrt{1+y^{\prime 2}}}}{1+y^{\prime 2}} \\ 0 &= y^{\prime\prime} \left(1-\frac{y^{\prime 2}}{1+y^{\prime 2}} \right) \end{aligned} $$
1.3.3 A mozgásegyenlet megoldása
Kaptunk egy szép másodrendű differenciálegyenletet a "mozgásra". Kicsit nézegetve ez kétféleképpen teljesülhet: egyrészt lehet a zárójel nulla $$ \begin{aligned} \left(1-\frac{y^{\prime 2}}{1+y^{\prime 2}} \right) = 0 \\ 1+y^{\prime 2} =y^{\prime 2} \\ 1 = 0 \end{aligned} $$ Szóval mégsem lehet az a zárójel nulla. Másrészt lehetséges megoldás még $$ \begin{aligned} y^{\prime\prime}(x) &= 0 \\ y^\prime(x) &= m \\ y(x) &= m x + b \end{aligned} $$ az egyenes.
1.3.4 A szebb megoldás
Ehelyett, vegyük észre hogy az Euler-Lagrange egyenlet jobb oldala nulla: $$ \begin{aligned} \frac{\rd}{\rd x} \frac{\partial \mathcal{L}}{\partial y^\prime} = \frac{\partial \mathcal{L}}{\partial y} =0 \end{aligned} $$ tehát $$ \frac{\partial \mathcal{L}}{\partial y^\prime} = \frac{1}{2}\frac{2 y^\prime}{\sqrt{1+y^{\prime 2}}} = \text{konst.} $$ Még nevet nem adva a konstansnak, ez kicsit átírható: $$ \begin{aligned} \frac{y^\prime}{\sqrt{1+y^{\prime 2}}} &= \text{konst.} \\ \frac{y^{\prime 2}}{1+y^{\prime 2}} &= \text{konst.} \\ y^{\prime 2} &= \text{konst.} \\ y^\prime &= \text{konst.} \end{aligned} $$ amit nevezzünk el végre: $$ y^{\prime}(x) = m $$ Ezt integrálva $x$ szerint megkapjuk a gyönyörű megoldást, miszerint: $$ y = mx + b $$ tehát két pont között a legrövidebb út az egyenes.
1.4 példa: Brachisztokron
Egy egészen hasonló, de történelmi jelentősségű példát kapunk, ha kicsit módosítunk az előző feladaton. Az alapkérdésünk most az, hogy (homogén) gravitációs térben milyen görbe az, amin legurulva a legkevesebb időbe telik az út $A$ és $B$ között. A legkevesebb időre törekszünk, tehát ami minimalizálandó az $$ \mathcal{S} = \int_A^B \rd t $$ Felhasználva, hogy $v = s/t$, illetve az energiamegmaradásból kapott $$ \begin{aligned} \frac{1}{2} m v^2 = mg y \\ v = \frac{1}{\sqrt{2g y}} \end{aligned} $$ összefüggést, ez átírható egy útra vett integrállá: $$ \mathcal{S} = \frac{1}{\sqrt{2g}} \int_{A}^{B} \frac{1}{\sqrt{y}} \rd s $$ Már csak az a kérdés, hogy mi legyen $\rd s$. Az előző feladattal ellentétben most vehetjük a változónak $y$-t, aminek függvénye az $x$, amivel $$ \rd s^2 = [1 + x^{\prime 2}(y)] \rd y^2 $$ Így a hatásintegrálunk $$ \mathcal{S} = \frac{1}{\sqrt{2g}} \int_{y_A}^{y_B} \frac{\sqrt{1+x^{\prime 2}(y)}}{\sqrt{y}} \rd y $$ Erre kell most alkalmaznunk az Euler-Lagrange formulát, ügyelve arra hogy most $x$ és $y$ kicserélődtek.
Az integrál előtti szorzófaktorokat elhagyva a deriváltak: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial x} = 0 \quad \quad \frac{\partial \mathcal{L}}{\partial x^\prime} = \frac{1}{\sqrt{y}}\frac{x^\prime}{\sqrt{1 + x^{\prime 2}}} \end{aligned} $$ Az előző feladatból tanulva most nem számítjuk ki $\frac{\rd}{\rd y} \frac{\partial \mathcal{L}}{\partial x^\prime}$-et, mert a másik nulla: tudjuk tehát, hogy $$ \begin{aligned} \frac{1}{\sqrt{y}}\frac{x^\prime}{\sqrt{1 + x^{\prime 2}}} &= \text{konst.} \\ \frac{1}{y}\frac{x^{\prime 2}}{1 + x^{\prime 2}} &= \text{konst.} = \frac{1}{2a} \end{aligned} $$ ahol a konstans azért így van bevezetve, hogy később szép legyen a megoldás. Ez egy diffegyenlet, amit meg kell oldanunk. Kis rendezéssel $$ \begin{aligned} x^{\prime 2} &= \frac{y}{2a}+ \frac{y}{2a}x^{\prime 2} \\ x^{\prime 2} &= \frac{ \frac{y}{2a}}{1- \frac{y}{2a}} \\ x^{\prime 2} &= \frac{ y}{2a -y} \end{aligned} $$ Ami felintegrálható, mint $$ x = \int \sqrt{\frac{y}{2a-y}}\, \rd y $$
Hogy ezt megoldjuk, megsejtjük a jó $y\rightarrow \varphi$ változócserét a tankönyv segítségével, mint $$ y = a(1-\cos{\varphi}) $$ Amivel $$ \begin{aligned} \frac{\rd y}{\rd \varphi} = a \sin{\varphi} \quad\quad \longrightarrow && \rd y = a \sin{\varphi}\, \rd \varphi \end{aligned} $$ és $$ \frac{y}{2a-y} = \frac{a(1-\cos{\varphi})}{2a - a + a\cos{\varphi}} = \frac{1 - \cos{\varphi}}{1+\cos{\varphi}} $$ Beírva mindkettőt, az integrandus $$ \begin{aligned} a\sqrt{\frac{1 - \cos{\varphi}}{\cos{\varphi}}} \sin{\varphi} &= a \sqrt{\frac{1 - \cos{\varphi}}{1+\cos{\varphi}} \sin^2{\varphi}} \\ &= a \sqrt{\frac{\sin^2{\varphi} - \sin^2{\varphi}\cos{\varphi}}{1+\cos{\varphi}} } \\ &= a \sqrt{\frac{1 - \cos^2{\varphi} - \sin^2{\varphi}\cos{\varphi}}{1+\cos{\varphi}} } \\ &= a \sqrt{\frac{1 - \cos^2{\varphi} - \cos{\varphi} + \cos^3{\varphi}}{1+\cos{\varphi}} } \\ &= a \sqrt{\frac{(1+\cos{\varphi}(1-\cos{\varphi})^2)}{1+\cos{\varphi}} } \\ &= a (1-\cos{\varphi}) \end{aligned} $$ Amit már könnyebb kiintegrálni, mint $$ x = a \int (1-\cos{\varphi}) \rd \varphi = a \left( \varphi - \sin{\varphi} \right) + \text{konst.} $$
Innentől a pontos megoldás már csak kezdeti értékek kérdése. Legyenek ők $x_A = y_A = 0$, amikből $\varphi = 0$ következik, illetve a konstansunk is nulla lesz. A megoldásunk tehát a görbére: $$ \begin{aligned} x &= a\left( \varphi - \sin{\varphi} \right) \\ y &= a(1-\cos{\varphi}) \end{aligned} $$ ahol $\varphi$ parametrizálja a görbét. Ha eleget nézzük ezt a megoldást, szét tudjuk szedni pár darabra:
- a két változó rendre szinuszosan és koszinuszosa változik, ami valami körszerűre utal;
- $x$-hez viszont folyamatosan adódik egy extra $\varphi$ tag, ami eltolja.
1.5. példa: Gömbszimmetrikus törésmutató
Kicsit közelebb kerülve a fizikához, most a két pont között utazzon valami létező dolog is: a fény. A megszokott koordinátarendszertől cserébe távolodjunk, most vegyünk egy közeget, ahol a törésmutató $$ n(r) = n_0 \frac{R}{r} $$ módon változik: fordítóttan arányos az origótól való távolsággal. Felidézve a gömbi koordináták esetét, az ívelemnégyzet $$ \rd s^2 = \rd r^2 + r^2 \rd \varphi^2 $$ Már csak az a kérdés, hogy mi szerint szeretnénk integrálni. Két változónk van, $r$ és $\varphi$, amik az út mentén valahogyan függnek egymástól. Most egyszerűbb a feladathoz úgy nekiállni, hogy $r$ függ valahogyan a szögtől, tehát a sugárirányú megváltozást célszerű $$ \rd r = r^{\prime} \rd \varphi $$ alakban írni. Ezzel az ívelemnégyzet: $$ \rd s^2 = (r^{\prime 2} + r^2) \rd \varphi^2 $$ Beírva mindent, a hatásintegrálunk $$ \mathcal{S} = n_0 R \int_{\varphi_A}^{\varphi_B} \frac{\sqrt{r^{\prime 2} + r^2}}{r} \rd \varphi $$
Felismerve a Lagrange-függvényt, és kicsit átírva: $$ \mathcal{L} = \frac{\sqrt{r^{\prime 2} + r^2}}{r} = \sqrt{1 + \frac{r^{\prime 2}}{r^2}} $$ felírhatjuk az Euler-Lagrange-hoz szükséges deriváltakat: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial r} = \frac{1}{2} \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \times r^{\prime 2}\frac{-2 }{r^3} = - \frac{ r^{\prime 2}}{r^3} \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \\ \frac{\partial \mathcal{L}}{\partial r^\prime} = \frac{1}{2} \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \times \frac{1}{r^2} 2 r^\prime = \frac{r^\prime}{r^2} \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \end{aligned} $$ Itt már egyik sem nulla, nincs mese, kell venni az utóbbinak a teljes deriváltját. Ezt szerintem szorzatfüggvényként célszerű, lebontva lépésekre: $$ \begin{aligned} \frac{\rd }{\rd \varphi} \frac{r^\prime}{r^2} &= \frac{r^{\prime\prime}\times r^2 - r^{\prime}\times2 r r^\prime }{r^4} = \frac{1}{r^3}\left(r^{\prime\prime} r - 2 r^{\prime 2} \right) \\ \frac{\rd }{\rd \varphi} \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} &= -\frac{1}{2} \frac{1}{\left(1 + \frac{r^{\prime 2}}{r^2}\right)^{3/2}} \times \frac{2 r^\prime r^{\prime\prime} \times r^2 -r^{\prime 2} \times 2 r r^{\prime}}{r^4} \\ &=- \frac{1}{r^3} \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \frac{1}{1 + \frac{r^{\prime 2}}{r^2}}\left(r r^\prime r^{\prime\prime} - r^{\prime3} \right) \end{aligned} $$ Ha ezek megvannak, a teljes deriválthoz csak össze kell kombinálni őket: $$ \begin{aligned} \frac{\rd }{\rd \varphi} \frac{\partial \mathcal{L}}{\partial r^\prime} &= \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \times \frac{\rd }{\rd \varphi} \frac{r^\prime}{r^2} + \frac{r^\prime}{r^2} \times \frac{\rd }{\rd \varphi} \frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \\ &= \frac{1}{r^3}\frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \left(r^{\prime\prime} r - 2 r^{\prime 2} -\frac{r^\prime}{r^2} \frac{r r^\prime r^{\prime\prime} - r^{\prime3}}{1 + \frac{r^{\prime 2}}{r^2}} \right) \\ &= \frac{1}{r^3}\frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \left(r^{\prime\prime} r - 2 r^{\prime 2} -r^{\prime 2} \frac{r r^{\prime\prime} - r^{\prime 2}}{r^2 + r^{\prime 2}} \right) \end{aligned} $$ Végül pedig fel tudjuk írni a mozgást megvalósító pálya Euler-Lagrange egyenletét: $$ \begin{aligned} \frac{\rd }{\rd \varphi} \frac{\partial \mathcal{L}}{\partial r^\prime} - \frac{\partial \mathcal{L}}{\partial r} &= 0 \\ \frac{1}{r^3}\frac{1}{\sqrt{1 + \frac{r^{\prime 2}}{r^2}}} \left(r^{\prime\prime} r - 2 r^{\prime 2} -r^{\prime 2} \frac{r r^{\prime\prime} - r^{\prime 2}}{r^2 + r^{\prime 2}} + r^{\prime 2} \right) &= 0 \\ &\Uparrow \\ r^{\prime\prime} r - r^{\prime 2} -r^{\prime 2} \frac{r r^{\prime\prime} - r^{\prime 2}}{r^2 + r^{\prime 2}} &= 0 \end{aligned} $$
Kis átalakítással $$ r^{\prime\prime} r - r^{\prime 2} - \frac{r r^\prime r^{\prime\prime} - r^{\prime3}}{1 + \frac{r^{\prime 2}}{r^2}} = \left(r^{\prime\prime} r - r^{\prime 2}\right) \left(1- \frac{r^{\prime 2}}{r^2 + r^{\prime 2}}\right) = 0 $$ Láthatólag ez kétféleképpen teljesülhet. Az egyik opció: $$ \begin{aligned} \left(1- \frac{r^{\prime 2}}{r^2 + r^{\prime 2}}\right) &= 0 \\ r^2 + r^{\prime 2} &= r^{\prime 2} \\ r(\varphi) &= 0 \end{aligned} $$ Ami a triviális megoldás: nem történik semmi. A másik kissé izgalmasabb: $$ \begin{aligned} \left(r^{\prime\prime} r - r^{\prime 2}\right) &= 0 \end{aligned} $$ Keressük azokat az $r(\varphi)$ függvényeket, amelyek teljesítik ezt az egyenletet. Kissé átírva $$ \begin{aligned} r^{\prime\prime} r &= r^{\prime 2} \\ \frac{r^{\prime\prime}}{r} &= \frac{ r^{\prime 2} }{r^2} \end{aligned} $$
Nem baj, ha ezt még nem látjuk mi lesz. A jobb oldal minden esetre egészen szép, szóval vezessünk be egy új $u$ függvényt, mint $$ u(\varphi) = \frac{r^\prime}{r} $$ Mi lesz az ő deriváltja? $$ u^\prime = \frac{\rd }{\rd \varphi} \frac{r^\prime}{r} = \frac{r^{\prime\prime} \times r - r^\prime \times r^\prime}{r^2} = \frac{r^{\prime\prime}}{r} - \frac{r^{\prime 2}}{r^2} $$ A fentiek alapján viszont ennek a jobb oldala nulla. Ergo $$ \begin{aligned} u^\prime = 0 \quad\quad \longrightarrow \quad\quad u = \text{konst.} = c \end{aligned} $$ Visszaírva az $u$ definíciójába $$ \begin{aligned} \frac{r^\prime}{r} = c \quad\quad \longrightarrow \quad\quad r(\varphi) = A \exp{(c \varphi)} \end{aligned} $$
Ezt láthatólag nem volt könnyű megoldani. Itt bukik elő a variációszámítás egyik hátránya: attól, hogy könnyen fel tudjuk írni a mozgásegyenletet, nem biztos, hogy azt egyszerűen (vagy egyáltalán) meg is tudjuk oldani. A következő órákon erre a feladatra látni fogunk majd egy kevésbé favágó módszert, ami (mint a legtöbb szép megoldás a fizikában) a szimmetriákra alapul.