Elmecha
2. óra Letöltés
Elméleti frissítő
A Lagrange-i mechanika kezdeteként feltettük, hogy léteznek valamilyen $\mathcal{L}$ Lagrange-függvények, amelyekből össze tudunk tákolni egy hatást $$ \mathcal{S} = \int_{t_1}^{t_2} \mathcal{L}(\vec{r}(t), \dot{\vec{r}}(t)\textcolor{gray}{,t})\, \rd t $$ amely ha stacionárius $$ \delta \mathcal{S} = 0 $$ akkor a megoldások a fizikai valóságot írják le. Ezt megkövetelve, ha alkalmazzuk a funkcionális deriválás szabályait, kapunk egy szép egyenletet magára az $\mathcal{L}$ Lagrange-függvényünkre: $$ \boxed{\frac{\rd}{\rd t} \frac{\partial \mathcal{L}(r(t), \dot{r}(t))}{\partial \dot{r}(t)} = \frac{\partial \mathcal{L}(r(t), \dot{r}(t))}{\partial r(t)}} $$ az Euler-Lagrange-egyenletet. Múlt órán néztünk pár gondolkodást igénylő geometriai példát, ahol ezt a Lagrange-függvényt nekünk kellett kitalálni úgy, hogy az adott feladatot írja le. Szerencsére a továbbiakban ez könnyebb lesz.
Klasszikus mechanika
Térjünk át a tipikus mechanikai feladatokra. Ekkor a hatásunk alakja $$ \mathcal{S} = \int \mathcal{L}(\vec{r}(t),\dot{\vec{r}}(t)) \rd t = \int \left(K(\dot{\vec{r}}, \textcolor{gray}{\vec{r}})-V(\vec{r})\right) \rd t $$ mert akkor az Euler-Lagrange egy ismerős egyenletre vezet: $$ \frac{\rd}{\rd t} \vec{p} = \boxed{\frac{\rd}{\rd t} \frac{\partial \mathcal{L}}{\partial \dot{\vec{r}}} = \frac{\partial \mathcal{L}}{\partial \vec{r}}} = - \nabla V(\vec{r}) $$ Ez hasznos, mert a kinetikus és a potenciális energiákat már ismerjük: az előbbi mindig $\frac{1}{2} m \dot{\vec{r}}^2$, a második pedig a rendszerből adódik. Ezt kihasználva tetszőleges mechanikai feladatokra fel tudjuk írni a Lagrange-függvényt a kinetikus és potenciális energiákat építőkockaként használva.
2.1. példa: Csúszó ék
Első példaként vegyünk egy asztalt. Rakjunk rá egy háromszög alakú, $M$ tömegű éket, ami súrlódás mentesen tud rajta mozogni. Erre az ékre pedig rakjunk rá egy $m$ tömegű téglatestet, ami szintén súrlódás nélkül le tud csúszni rajta. Ha engedjük lecsúszni a kis téglatestet, mekkora lesz az ék gyorsulása? Kezdjük az első lépéssel:
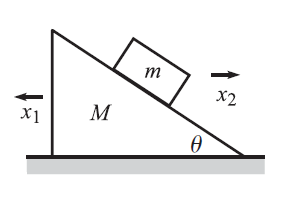
1.1.1. Mi a hatás?
Kell nekünk a $\mathcal{L}$ Lagrange-függvényünk két része: a kinetikus és a potenciális energia. Az utóbbi itt könnyebb: ahogy csúszik lefele a téglatest, csökken a gravitációs potenciálja. Tehát: $$ \Delta V = mg \Delta h $$ amit paraméterezni kell majd valahogy szépen. Addig is emlékezzünk, hogy bárhol megválaszthatjuk a nullpontját, de lefelé menve csökkenni fog.
A kinetikus energiánk már picit több tagból áll: az $m$ test is tud mozogni és az $M$ is. Tehát: $$ K = \frac{1}{2}M \dot{x_1}^2 + \frac{1}{2}M \dot{y_1}^2 + \frac{1}{2} m \dot{x_2}^2 + \frac{1}{2} m \dot{y_2}^2 $$ Ami általánosan szép és jó, viszont elviekben még semmi nem zárja ki, hogy a kis téglatestünk egyenesen átessen a háromszögön, a nagy háromszögünk pedig az asztalon. Ehhez egy-egy kényszert kell kiróni: az $m$ test kényszeresen az ék felületén közlekedik lefelé, az $M$ test pedig egyáltalán nem mozoghat fel-le.
Ahhoz, hogy ez a kényszer teljesüljön, matekká kell fogalmazni amit szeretnénk kiróni. Kezdjük a háromszöggel: ha valami nem mozoghat fel-le, akkor $$ y_1 = \text{konst.} \quad\quad \longrightarrow \quad\quad \dot{y_1} = 0 $$ A kis téglatestünk úgy közlekedik lefelé, hogy végig a háromszög élén marad. Ehhez segítségül hívjuk az ábrát. Azt látjuk, hogy össze tudjuk kötni a kis téglatest $y$ irányú, $y_2$ mértékű lecsúszását azzal, hogy mennyit mozogtak $x$ irányba a testek. Kis matekkal: $$ y_2 = (x_1+x_2) \tan{\varphi} $$
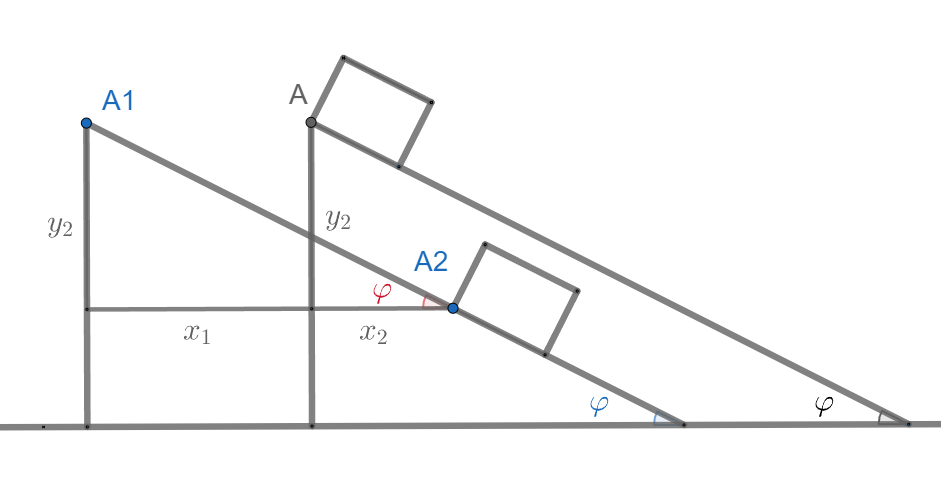
Ez kétrétről is hasznos lesz: egyrészt a potenciális energiába pont ezt a magasságmegváltozást kerestük: $$ \Delta V = - mg y_2 $$ másrészt pedig be tudjuk helyettesíteni a kinetikus energiába is, mivel $$ \dot{y_2} = (\dot{x_1}+\dot{x_2}) \tan{\varphi} $$ Felírva tehát, a teljes Lagrange-függvény: $$ \mathcal{L} = \frac{1}{2}M \dot{x_1}^2 + \frac{1}{2} m \dot{x_2}^2 + \frac{1}{2} m (\dot{x_1}+\dot{x_2})^2 \tan^2{\varphi} + mg (x_1+x_2) \tan{\varphi} $$
2.1.2. Mik a mozgásegyenletek?
Két testünk mozog ebben a rendszerben, amiknek az $(x_1, \dot{x_1})$ és $(x_2, \dot{x_2})$ koordinátáival felírtuk a hatást. Hogy megkapjuk a mozgásegyenleteket, egyszerűen az Euler-Lagrange egyenleteket kell felírnunk a két testre. Kezdve az elsővel: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial x_1}= mg \tan{\varphi} \quad \frac{\partial \mathcal{L}}{\partial \dot{x_1}}=M\dot{x_1} + m \tan^2{\varphi} (\dot{x_1}+\dot{x_2}) \end{aligned} $$ tehát az ék mozgásegyenlete: $$ mg \tan{\varphi} = M \ddot{x_1} + m \tan^2{\varphi}(\ddot{x_1}+\ddot{x_2}) $$ A kis téglatestünkre is fel lehet írni ugyanezeket: vegyük észre, hogy szinte teljesen szimmetrikus a Lagrange-ünk, annyi a különbség a két változó közt, hogy a kitneikus tagban más tömeg szerepel. A kis $m$ tömegű test egyenlete tehát: $$ mg \tan{\varphi} = m \ddot{x_2} + m \tan^2{\varphi}(\ddot{x_1}+\ddot{x_2}) $$
2.1.3. Mi a pálya?
Hogy megkapjuk a trajektóriákat, meg kell oldanunk a mozgásegyenleteket. Na, ez az a lépés ami általánosságban nem lehetséges algebrailag. Szerencsére viszont léteznek feladatgyűjtemények olyan példákkal amikre igen: ez például pont megoldható. Vegyük a két mozgásegyenlet különbségét: $$ \begin{aligned} 0 &= M \ddot{x_1} - m \ddot{x_2} \\ 0 &= \frac{\rd}{\rd t} \left(p_{1,x} - p_{2,x}\right) \end{aligned} $$ ami igazából ismerős lehet: $$ p_{1,x} - p_{2,x} = \text{konst.} $$ ez nem más, mint az $x$ irányú lendület megmaradása (a fordított előjelet az okozza, hogy az ék elmozdulását ellenkező irányúnak vettük fel a téglatestéhez képest). Visszaidézve az első órát, itt is láthatjuk, hogy eltolásinvariáns a rendszerünk erre az irányra, amivel ez az eredmény konzisztens.
Minden esetre, megvan a két egyenlet amit meg kell oldani. Ezeket kicsit átrendezve: $$ \begin{aligned} mg \tan{\varphi} - m \tan^2{\varphi}\ddot{x_2} &= (M + m \tan^2{\varphi})\ddot{x_1} \\ mg \tan{\varphi} - m \tan^2{\varphi}\ddot{x_1} &= m(1 + \tan^2{\varphi})\ddot{x_2} \end{aligned} $$ be tudjuk helyettesítni az elsőbe $\ddot{x_2}$-t, amivel $$ \begin{aligned} (M + m \tan^2{\varphi})\ddot{x_1} &= mg \tan{\varphi} - m \tan^2{\varphi} \frac{g \tan{\varphi} - \tan^2{\varphi}\ddot{x_1}}{(1 + \tan^2{\varphi})} \\ \left(M + m \tan^2{\varphi} - m\frac{\tan^4{\varphi}}{1 + \tan^2{\varphi}}\right)\ddot{x_1} &= mg \tan{\varphi} - m \tan^2{\varphi} \frac{g \tan{\varphi}}{1 + \tan^2{\varphi}} \end{aligned} $$ Vegyük észre hogy $1+\tan^2 = 1/\cos^2$, így pár szögfüggvényes egyszerűsítés után $$ \begin{aligned} \left(M + m \tan^2{\varphi} - m\frac{\sin^4{\varphi}}{\cos^2{\varphi}}\right)\ddot{x_1} &= mg \tan{\varphi} - m \sin^2{\varphi} g \tan{\varphi} \\ \left(M + m \sin^2{\varphi}\frac{1- \sin^2{\varphi}}{\cos^2{\varphi}}\right)\ddot{x_1} &= mg \tan{\varphi} (1 - \sin^2{\varphi}) \\ \left(M + m \sin^2{\varphi}\right)\ddot{x_1} &= mg \tan{\varphi} \cos^2{\varphi} \\ \left(M + m \sin^2{\varphi}\right)\ddot{x_1} &= mg \cos{\varphi}\sin{\varphi} \\ \ddot{x_1} &= \frac{mg \cos{\varphi}\sin{\varphi}}{M + m \sin^2{\varphi}} \end{aligned} $$ amivel meg is válaszoltuk a kérdést: ezzel a konstans gyorsulással fog mozogni az ékünk.
Ha a mozgás időfüggésére vagyunk kíváncsiak, akkor ezt még ki kell integrálni kétszer. Emlékeztetőül $$ \begin{aligned} \ddot{x_1} &= a_1 \\ \int \ddot{x_1} \rd t &= \int a_1 \rd t \\ \dot{x_1} &= a_1 t \\ \int \dot{x_1} \rd t &= \int a_1 t\, \rd t \\ x_1(t) &= \frac{a_1}{2} t^2 +c_1 \end{aligned} $$ A másik pedig ugyanígy, $a_2 = \frac{M}{m} a_1$ gyorsulással.
2.2 példa: Félkörről lecsúszás - 1
Vegyünk egy asztalt, és szögezzünk rá egy félkört. Ezután rakjunk rá egy kis tömegpontot, ami súrlódásmentesen lecsúszhat: mi lesz a mozgásegyenlet?
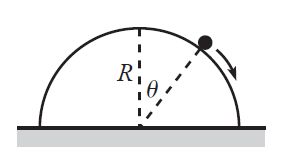
Először írjuk fel a feladatot Descartes-i koordinátarendszerben. Kényszerek nélkül, a kinetikus tagban lehetne bármi: $$ K = \frac{1}{2} m \dot{x}^2 + \frac{1}{2} m \dot{y}^2 $$ a potenciális energiánkat pedig felvehetjük, mint $$ V = -mg (R-y) $$ Persze tudjuk, hogy a mozgás itt csak a félkör felületén történhet: ez matekul annyit tesz, hogy $$ x^2 + y^2 = R^2 $$ Ezzel pedig ki tudjuk fejezni valamelyik változónkat a másik függvényében. Legyen most ez $x(y)$, mert a potenciális energiában már amúgy is $y$ van. $$ x = \sqrt{R^2 - y^2} $$ Az ő deriváltja: $$ \dot{x} = \frac{y \dot{y}}{\sqrt{R^2 - y^2}} $$ Így a Lagrange-unk: $$ \mathcal{L} = \frac{1}{2}m \dot{y}^2 \left( 1 + \frac{y^2}{R^2 - y^2}\right) + mg(R-y) $$
Ha ezzel megvagyunk, felírhatjuk az Euler-Lagrange egyenlet két tagját: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial y} = \frac{1}{2}m \dot{y}^2 \frac{2y(R^2 - y^2)+2y^2\cdot y}{(R^2 - y^2)^2} - mg \quad \quad \frac{\partial \mathcal{L}}{\partial \dot{y}} = m \dot{y} \left( 1 + \frac{y^2}{R^2 - y^2}\right) \end{aligned} $$ amihez még deriválni kell egyet: $$ \frac{\rd}{\rd t} \frac{\partial \mathcal{L}}{\partial \dot{y}} = m \left[ \ddot{y} \left( 1 + \frac{y^2}{R^2 - y^2}\right) + \dot{y}^2\frac{2y(R^2 - y^2) +2 y^3 }{(R^2 - y^2)^2} \right] $$ Egyenlővé téve amit kell, és kicsit átalakítva: $$ \begin{aligned} \frac{1}{2}m \dot{y}^2 \frac{2y(R^2 - y^2)+2y^2\cdot y}{(R^2 - y^2)^2} - mg &= m \left[ \ddot{y} \left( 1 + \frac{y^2}{R^2 - y^2}\right) + \dot{y}^2\frac{2y(R^2 - y^2) +2 y^3 }{(R^2 - y^2)^2} \right] \\ \dot{y}^2 \frac{y(R^2 - y^2)+y^3}{(R^2 - y^2)^2} - g &= \ddot{y} \left( 1 + \frac{y^2}{R^2 - y^2}\right) + 2\dot{y}^2\frac{y(R^2 - y^2) + y^3 }{(R^2 - y^2)^2} \\ - \dot{y}^2 \frac{y(R^2 - y^2)+y^3}{(R^2 - y^2)^2} - g &= \ddot{y} \left( 1 + \frac{y^2}{R^2 - y^2}\right) \end{aligned} $$ Ez nem túl szép. Vezessük be a tömegpont helyzetét leíró szöget, amivel $$ y = R \cos{\varphi} $$
Ennek hála $$ \begin{aligned} R^2 - y^2 = R^2(1-\cos^2{\varphi}) = R^2 \sin^2{\varphi} \end{aligned} $$ Beírva a mozgásegyenletbe, leegyszerűsödik pár dolog: $$ \begin{aligned} - \dot{y}^2 y \frac{ R^2 \sin^2{\varphi}+y^2}{(R^2 \sin^2{\varphi})^2} - g &= \ddot{y} \left( 1 + \frac{R^2 \cos^2{\varphi}}{R^2 \sin^2{\varphi}}\right) \\ - \dot{y}^2 y \frac{ R^2 \sin^2{\varphi}+R^2 \cos^2{\varphi}}{(R^2 \sin^2{\varphi})^2} - g &= \ddot{y} \left( \frac{R^2 \sin^2{\varphi}+R^2 \cos^2{\varphi}}{R^2 \sin^2{\varphi}}\right) \\ - \dot{y}^2 y \frac{ 1 }{R^2 \sin^4{\varphi}} - g &= \ddot{y} \left( \frac{1}{ \sin^2{\varphi}}\right) \end{aligned} $$ Beírva végül, hogy $$ \begin{aligned} \dot{y} = - R \sin{\varphi} \dot{\varphi} \quad \quad \ddot{y} = -R (\dot{\varphi}^2\cos{\varphi} + \sin{\varphi} \ddot{\varphi}) \end{aligned} $$ Először $$ \begin{aligned} - R^3 \dot{\varphi}^2 \sin^2{\varphi} \cos{\varphi} \frac{ 1 }{R^2 \sin^4{\varphi}} - g &= \ddot{y} \left( \frac{1}{ \sin^2{\varphi}}\right) \\ - \dot{\varphi}^2 R \frac{ \cos{\varphi} }{\sin^2{\varphi}} - g &= \ddot{y} \left( \frac{1}{ \sin^2{\varphi}}\right) \end{aligned} $$ aztán $$ \begin{aligned} - \dot{\varphi}^2 R \cos{\varphi} - g \sin^2{\varphi} &= - R (\dot{\varphi}^2\cos{\varphi} + \sin{\varphi} \ddot{\varphi}) \\ \ddot{\varphi} &= \frac{g}{R}\sin{\varphi} \end{aligned} $$
Ezt nem triviális megoldani, szóval egyelőre így hagyjuk. Láthatóan egy hosszadalmas feladattal küzdöttünk meg, amin az segített, hogy áttértünk egy új változóra a szög segítségével. Sok fáradalmat megspórolhatunk a jövőben, ha ezt ezek után hamarabb megtesszük, például már a legelején.
Általános koordináták
Eddig a Descartes-i koordinátákban mozogtunk, de ennek különös fizikai szerepe nincsen: bármely más koordinátarendszerben is szeretnénk, hogy a fizika érvényes legyen. A variációs módszereknek itt jön be mégegy előnye a Newtoni mechanikával szemben: a mozgást leíró egyenletünk pont ugyanúgy néz ki (szinte) minden koordinátarendszerben. Általános $q$ koordinátákkal: $$ \mathcal{S} = \int \mathcal{L}(q(t), \dot{q}(t)) \rd t $$ lesz a hatásunk, amire az Euler-Lagrange alakja változatlan $$ \frac{\partial \mathcal{L}}{\partial q} = \frac{\rd}{\rd t} \frac{\partial \mathcal{L}}{\partial \dot{q}} $$ Nézzünk is egy pár példát, ahol látjuk ennek a jelentősségét.
2.3. példa: Félkörről lecsúszás - 2
Jól látható ennél a feladatnál, hogy sokat egyszerűsít, ha áttérünk a konfigurációnkhoz jobban illeszkedő változóra: a szögre. Ezt az előbb a mozgásegyenlet levezetése után tettük meg. A Lagrange-i mechanikában viszont rögtön az első lépésben, a hatás felírásánál is tudunk élni ezzel az egyszerűsítéssel. A változónak most a szöget véve, a kinetikus energiánk: $$ \begin{aligned} K &= \frac{1}{2}m \dot{y}^2 \left( 1 + \frac{y^2}{R^2 - y^2}\right) \\ &= \frac{1}{2}m R^2 \sin^2{\varphi} \dot{\varphi}^2 \left(1+ \frac{R^2 \cos^2{\varphi}}{R^2 \sin^2{\varphi}} \right) \\ &= \frac{1}{2}m \dot{\varphi}^2 R^2 \sin^2{\varphi} \left(\frac{R^2}{R^2 \sin^2{\varphi}} \right) \\ &= \frac{1}{2}m \dot{\varphi}^2 R^2 \end{aligned} $$ Amit most behelyettesítve számoltunk ki, de egyébként abból is kiindulhattunk volna, hogy mi az érintőirányú sebesség egy kör mentén (sugár $\cdot$ szögsebesség). Én inkább a behelyettesítéses számolást ajánlom: lesznek olyan példák, ahol az utóbbi módszer félrevezet, ha nem vagyunk óvatosak. A potenciális energia szintén egyszerű: $$ \begin{aligned} V &= -mg y \\ &= -mg R(1- \cos{\varphi}) \\ &= -mgR + mgR \cos{\varphi} \end{aligned} $$ használjuk ki, hogy ez tetszőlegesen eltolható egy konstanssal, és legyen: $$ V = mgR \cos{\varphi} $$
Így a Lagrange-unk szép tömör alakot ölt: $$ \mathcal{L} = \frac{1}{2}m \dot{\varphi}^2 R^2 - mgR \cos{\varphi} $$ És az Euler-Lagrange is egyszerűbb: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial \varphi} = mgR \sin{\varphi} \quad \quad \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = m R^2 \dot{\varphi} \end{aligned} $$ amiből egy deriválás után $$ m R^2 \ddot{\varphi} = mgR \sin{\varphi} $$ Tehát a mozgásegyenlet: $$ R \ddot{\varphi} = g \sin{\varphi} $$
Ez jóval kevesebb lépésbe került, mint derékszögű koordinátákkal. Ez az egyenlet pár trükkel megoldható, de helyette most nézzünk meg egy speciális esetet: mi van a félgömb tetejéhez közel, ahol $\varphi \ll 1$? $$ \sin{\varphi} \approx \varphi $$ Tehát $$ \ddot{\varphi} \approx \frac{g}{R} \varphi $$ Ez egy nevezetes diffegyenlet: valamilyen függvény második deriváltja arányos önmagával. Megoldása: $$ \varphi (t) \approx c_1 e^{\sqrt{\frac{g}{R}} t} + c_2 e^{-\sqrt{\frac{g}{R}} t} $$
Energiamegmaradás
A gyakorlatban az egy dimenziós példák gyakran még tovább egyszerűsödnek. Mindeddig nem használtunk ki egy erős eszközt: az energiamegmaradást. Ugyanis ha a Lagrange-függvényünk nem függ expliciten az időtől, akkor létezik egy mennyiség, ami megmarad: őt (általánosított) energiának hívjuk. $$ \mathcal{L}\bigl(r(t), \dot{r}(t)\bigr) \quad\quad \longrightarrow \quad\quad E = \dot{\vec{r}} \frac{\partial \mathcal{L}}{\partial \dot{\vec{r}}} - \mathcal{L} = \text{konst.} $$ Ennek egy speciális esete a klasszikus mechanika, ugyanis ekkor $$ E = K+V $$ az energia nem más mint a kinetikus és potenciális energiák összege.
Ha őt kihasználjuk, minden eddig vett példa leegyszerűsödik; és új feladatok válnak könnyen (vagy legalábbis könnyebben) megoldhatóvá. Nézzük például az előzőt!
2.4. példa: Félkörről lecsúszás - 3
Idézzük vissza a Lagrange-függvényünket: $$ \mathcal{L} = \frac{1}{2}m \dot{\varphi}^2 R^2 - mgR \cos{\varphi} $$ És a belőle kapott lendületet: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = m R^2 \dot{\varphi} \end{aligned} $$ Használjuk ki az energiamegmaradást! Ez felírva $$ \begin{aligned} \dot{\varphi} \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} - \mathcal{L} &= E \\ m R^2 \dot{\varphi}^2 - \frac{1}{2}m \dot{\varphi}^2 R^2 + mgR \cos{\varphi} &= E \\ \frac{1}{2}m \dot{\varphi}^2 R^2 + mgR \cos{\varphi} &= E \end{aligned} $$ Nem lepődünk meg, hogy tényleg $K+V$ alakú. Az energia viszont konstans: vegyük referencia értéknek azt, amikor fent csücsül a golyó és $E = mgR$. Ezt beírva, és kicsit átírogatva az egyenletet: $$ \begin{aligned} \frac{1}{2}m \dot{\varphi}^2 R^2 &+ mgR \cos{\varphi} = mgR \\ \dot{\varphi}^2 &= \frac{2g}{R} (1- \cos{\varphi}) \\ \dot{\varphi} &= \pm\sqrt{2} \sqrt{\frac{g}{R}} \sqrt{1- \cos{\varphi}} \end{aligned} $$
Egy elsőrendű diffegyenletet kaptunk. Most ezt oldjuk, meg, hogy gyakoroljuk a diffegyenletek megoldását is. Először is a tömörség kedvéért legyen $\omega = \sqrt{g/R}$, és nézzük csak a pozitív megoldást. $$ \begin{aligned} \frac{\rd \varphi}{\rd t} = \sqrt{2}\, \omega\sqrt{1- \cos{\varphi}} \\ \rd \varphi = \sqrt{2}\, \omega\sqrt{1- \cos{\varphi}} \rd t \\ \frac{1}{\sqrt{1- \cos{\varphi}}}\rd \varphi = \sqrt{2}\, \omega \rd t \\ \int \frac{1}{\sqrt{1- \cos{\varphi}}}\rd \varphi = \int \sqrt{2}\, \omega \rd t \end{aligned} $$ Ennek mindkét oldala kiintegrálható, kezdjük a jobbal: $$ \int \frac{1}{\sqrt{1- \cos{\varphi}}}\rd \varphi = \sqrt{2}\, \omega t $$ A bal már nehezebb, ott már fordulhatunk szimbolikus integrálszámító programokhoz. Ha nem hagyatkoznánk a gépre, akkor viszont segítenek köztes lépésként a következő tippek: $$ \begin{aligned} 1-\cos{\varphi} = 2 \sin^2{\frac{\varphi}{2}}\\ u := \tan{\frac{\varphi}{4}} \end{aligned} $$ Ezekkel leredukálódik a problémánk $\int 1/u \rd u$ alakra, amit már meg tudunk oldani. Visszahelyettesítve mindent $$ \ln{\tan{\frac{\varphi}{4}}} + c = \omega t $$ Ezt még invertálni kell $\varphi(t)$-re: $$ \varphi(t) = 4 \arctan{\left(C e^{\omega t} \right)} $$ ahol a konstans $c$-t kicseréltük egy $C$-re. Ezzel megkaptuk az egzakt megoldásunkat, hála az energiamegmaradásnak.
2.5. példa: Rugós inga
Vegyünk egy sima matematikai ingát, ami alapjáraton $l$ hosszúságú, és egy $m$ tömegű testet tart. Cseréljük ki a madzagot egy $k$ rugóállandójú rugóra: mi lesz ekkor a mozgásegyenlet?
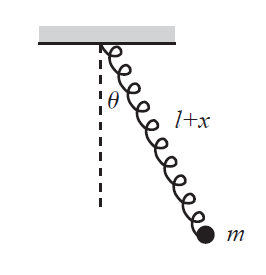
2.5.1. Descartes
Bemelegítésként először írjuk fel a sima inga problémáját Lagrange-osan, Descartes-i koordinátákkal. A kényszermentes Lagrange-függvény két tagja, ha origónak a felfüggesztési pontot vesszük: $$ \begin{aligned} K = \frac{1}{2} m \dot{x}^2 + \frac{1}{2} m \dot{y}^2 \\ V = - mg (l-y) \end{aligned} $$ Ezt még ki kell egészítenünk azzal a feltétellel, hogy a test csak az $l$ hosszúságú drót által rajzolt körön mozog. Most direkt távol maradva a szögektől, ez egy kis Pitagorasz tétel után: $$ \begin{aligned} l^2 = x^2 + y^2 \\ y = \sqrt{x^2 - l^2} \end{aligned} $$ tehát $$ \dot{y} = \frac{\rd}{\rd t} (\sqrt{x^2 - l^2}) = \frac{x \dot{x}}{\sqrt{x^2 - l^2}} $$ amivel $$ \dot{y}^2 = \frac{x^2 \dot{x}^2}{x^2 - l^2} $$
Beírva mindent a Lagrange-ba: $$ \mathcal{L}_{\text{inga}} = \frac{1}{2} m \dot{x}^2 \left( 1 + \frac{x^2 }{x^2 - l^2}\right) + mg (l- \sqrt{x^2 - l^2}) $$ És ez még csak maga az inga. Ha belevesszük a rugót is: $$ V_{\text{rugó}} = \frac{1}{2} k \Delta l^2 $$ ahol $\Delta l$ fejezi ki, hogy mennyire nyúlt meg a rugó az eredeti $l_0$-hoz képest. Descartes-i koordinátákkal: $$ \begin{aligned} x^2 + y^2 = l^2 = (l_0+\Delta l)^2 \\ \Delta l = \sqrt{x^2 + y^2} - l_0 \end{aligned} $$ amivel $$ V_{\text{rugó}} = \frac{1}{2} k \left(\sqrt{x^2 + y^2} - l_0 \right)^2 $$ És itt meg is állnék, mielőtt elkezdünk tovább helyettesítgetni. Szerintem sikerült demonstrálni, hogy mennyire el tudnak bonyolódni a tagok, ha a feladathoz rosszul illeszkedő koordinátarendszert választunk. Nézzük meg, hogy hogyan kell ezt szépen megoldani.
2.5.2. Polár
Hogy kiválasszuk a jó koordinátákat, gondolkodjunk kicsit a feladaton. Két dolgunk van: ingánk és rugónk. Az inga nagyon illeszkedik a poláros koordinátázáshoz. A rugóban pedig az jelenik meg, hogy mennyit nyúl meg sugárirányban. Legyen a két változónk $\varphi$, az inga kitérési szöge, és $R$, az inga megnyúlása az eredeti $l_0$ hosszához képest. A régi változók nyelvén tehát: $$ \begin{aligned} x^2 + y^2 &= l^2 = (l_0 + R)^2 \\ x = l \sin{\varphi} &= (l_0 + R) \sin{\varphi} \\ y = l \cos{\varphi} &= (l_0 + R) \cos{\varphi} \end{aligned} $$ Milyen sebességek jelennek meg a kinetikus tagban? Lesz egyrészt a sugárirányú sebesség, ami azt mondja meg, hogy mennyire változik éppen $R$: $$ K_r = \frac{1}{2} m \dot{R}^2 $$ és lesz egy erre merőleges komponens, ami az érintő irányú sebesség lesz. Ez pedig a $\dot{\varphi}$ szögsebesség szorozva a $(l_0+R)$ sugárral, tehát $$ K_\varphi = \frac{1}{2} m (l_0+R)^2 \dot{\varphi}^2 $$ A rugó potenciális energiája így már nagyon egyszerű: $$ V_{\text{rugó}} = \frac{1}{2} k R^2 $$ Cserébe a gravitációs potenciális energiánk lesz picit csúnyább: $$ V_{\text{grav.}} = -mg (l_0+R) \cos{\varphi} $$ ahol az $y$ helyére behelyettesítettük az új koordinátákat.
Egy szó mint száz, kész is a Lagrange-unk: $$ \mathcal{L} = \frac{1}{2} m \dot{R}^2 + \frac{1}{2} m (l_0+R)^2 \dot{\varphi}^2 + mg (l_0+R) \cos{\varphi} - \frac{1}{2} k R^2 $$ és jöhetnek is az Euler-Lagrange egyenletek. Két változónk van, tehát kettő lesz: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial R} = m(l_0+R)\dot{\varphi}^2 + mg \cos{\varphi} - kR && \frac{\partial \mathcal{L}}{\partial \dot{R}} = m \dot{R} \\ \frac{\partial \mathcal{L}}{\partial \varphi} = - mg (l_0+R) \sin{\varphi} && \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = m(l_0+R)^2 \dot{\varphi} \end{aligned} $$ Amikkel elvégezve a deriválásokat: $$ \begin{aligned} (l_0+R)\dot{\varphi}^2 + g \cos{\varphi} - \frac{k}{m}R = &\ddot{R} \\ - g (l_0+R) \sin{\varphi} = 2(l_0+R)\dot{R} \dot{\varphi} + (l_0+R)^2& \ddot{\varphi} \end{aligned} $$ Kicsit még szépítve: $$ \begin{aligned} \ddot{R} &= (l_0+R)\dot{\varphi}^2 + g \cos{\varphi} - \frac{k}{m}R \\ (l_0+R) \ddot{\varphi} &= - 2\dot{R} \dot{\varphi} - g \sin{\varphi} \end{aligned} $$ Ezt már be lehet küldeni a kedvenc numerikus megoldónknak, és meg is lesznek a pályák.
Teljes derivált
Előadáson elhangzott, hogy a fizika invariáns marad arra, ha a Lagrange-függvényhez hozzáadunk egy teljes deriváltat: $$ \mathcal{L} \quad \longrightarrow \quad \mathcal{L}^\prime =\mathcal{L}+\frac{\rd F}{\rd t} $$ feltéve hogy a függvény alakja $F(t, q)$, tehát csak a koordinátáktól és az időtől függhet, a sebességektől nem. Ezt gyorsan bebizonyítjuk, belátva hogy az Euler-Lagrange egyenlet ekkor is teljesül: $$ \begin{aligned} \frac{\rd }{\rd t} \frac{\partial \mathcal{L}^\prime}{\partial \dot{q}} &= \frac{\partial \mathcal{L}^\prime}{\partial q} \\ \frac{\rd }{\rd t} \left[ \frac{\partial \mathcal{L}}{\partial \dot{q}} + \frac{\partial}{\partial \dot{q}} \dot{F}\right] &= \frac{\partial \mathcal{L}}{\partial q} + \frac{\partial \dot{F}}{\partial q} \end{aligned} $$ Mindkét oldalról kiesik az első tag, hála a sima, teljes derivált nélküli Euler-Lagrange egyenletnek. Ami marad: $$ \frac{\rd }{\rd t} \frac{\partial}{\partial \dot{q}} \dot{F} =\frac{\partial \dot{F}}{\partial q} $$ Ennek a tovább fejtéséhez először is nézzük meg hogyna néz ki $F$ teljes időderiváltja, $\dot{F}$. Mivel $F(t,q)$ alakú, ezért két módon függhet az időtől: expliciten $t$-n keresztül, és impliciten $q(t)$-n át. Tehát $$ \dot{F} = \frac{\partial F}{\partial q} \frac{\partial q}{\partial t} + \frac{\partial F}{\partial t} = \frac{\partial F}{\partial q} \dot{q} + \frac{\partial}{\partial t} F $$ Hogy függhet ez a kifejezés $\dot{q}$-től? Mivel $F$ önmagában sehogy, egyetlen helyen hat a $\dot{q}$ szerinti parciális deriválás: $$ \frac{\partial}{\partial \dot{q}}\dot{F} = \frac{\partial F}{\partial q}\cdot 1 +0 $$ Alkalmazzuk ugyanezt a logikát most $F$ helyett az így kapott $\frac{\partial F}{\partial q}$-ra: $$ \frac{\rd}{\rd t} \frac{\partial F}{\partial q} = \frac{\partial}{\partial q} \frac{\partial F}{\partial q} \dot{q} + \partial_t \frac{\partial F}{\partial q} $$ A parciális deriváltak egymással felcserélhetők egy szép tételnek hála, így összességében $$ \begin{aligned} \frac{\rd}{\rd t} \frac{\partial F}{\partial q} &= \frac{\partial}{\partial q} \frac{\partial F}{\partial q} \dot{q} + \frac{\partial}{\partial q} \frac{\partial F}{\partial t} \\ &=\frac{\partial }{\partial q} \left[ \frac{\partial F}{\partial q} \dot{q} + \frac{\partial F}{\partial t} \right] \\ &= \frac{\partial \dot{F}}{\partial q} \end{aligned} $$ amivel be is bizonyítottuk a feltevésünket.
2.6. példa: Egy csúnyának tűnő feladat
A gonosz feladatgyűjtemény a következő Lagrange-függvénnyel szembesít minket: $$ \mathcal{L}(x,\dot{x},t) = \dot{x}^2 - (x+t)^2 - \dot{x} t^2 $$ majd azt kéri, hogy használjuk az energiamegmaradást a feladat megoldására. Ez egy hibának tűnhet, mert a Lagrange explicit időfüggő: ekkor nem maradhat meg az energia. Oldjuk meg mégis, a most tanult új trükköt alkalmazva.
Először is bontsuk szét a zárójelet: $$ \mathcal{L}(x,\dot{x},t) = \dot{x}^2 - x^2 - 2xt - t^2 - \dot{x} t^2 $$ A keverten $t$-t és $x$-et tartalmazó tagokkal van probléma, őket szeretnénk eltűntetni. Ilyenkor az ember próbálkozik pár függvénnyel, amíg nem talál valamit, ami közelebb viszi a jó megoldáshoz. Legyen az első tippünk $$ F(x,t) = \frac{1}{3}t^3 $$ Ezt lederiválva és hozzáadva a Lagrange-hoz eltűnik a $t^3$ tag. Második próbálkozásunk pedig legyen $$ G(x,t) = x t^2 \quad \longrightarrow \quad \dot{G} = \dot{x}t^2 + 2tx $$ amivel már boldogak lehetünk: ezt a két teljes deriváltat hozzáadva eltűntek az expliciten időfűggő tagok a Lagrange-ból. Ami maradt: $$ \mathcal{L}^\prime = \dot{x}^2 - x^2 $$ már megoldható az energiamegmaradást használva.
Itt nem feltétlen egyértelmű hogy egy klasszikus mechanikai feladatról van szó, ezért a $K+V$ helyett használjuk az általánosabb képletet: $$ E = \dot{x} \frac{\partial \mathcal{L}}{\partial \dot{x}} - \mathcal{L} = 2 \dot{x}^2 - \left(\dot{x}^2 - x^2 \right) = \dot{x}^2 + x^2 $$ Ami egy megmaradó mennyiség. Vegyük fel a nullpontját úgy, hogy $E = 1$ teljesüljön. Ekkor a megoldandó differenciálegyenletünk $$ \begin{aligned} \dot{x}^2 = 1- x^2 \\ \dot{x} = \sqrt{1-x^2} \end{aligned} $$ Ez egy szeparálható diffegyenlet: $$ \begin{aligned} \frac{\rd x}{\rd t} = \sqrt{1-x^2} \\ \rd x = \sqrt{1-x^2}\, \rd t \\ \frac{\rd x}{\sqrt{1-x^2}} = \rd t \\ \int \frac{\rd x}{\sqrt{1-x^2}} = \int \rd t \\ \arcsin{x} = t+c \\ x = \sin{(t+c)} \end{aligned} $$ Méghozzá a harmonikus mozgásé.