Elmecha
3. óra Letöltés
Ciklikus koordináták
A mai órán további megmaradó mennyiségekkel foglalkozunk: ezeknek első példája a ciklikus koordinátákra vezethető vissza. Velük már találkoztunk, csak nem nevesítettük őket. Ha a Lagrange alakja $$ \mathcal{L}(x,y,\dot{x},\dot{y}) = \mathcal{L}(x,\dot{x},\dot{y}) = K(\textcolor{gray}{x},\dot{x},\dot{y})-V(x) $$ tehát az egyik koordinátát nem tartalmazza expliciten, akkor az a koordináta ciklikus. Ekkor a rá vonatkozó Euler-Lagrange egyenlet alapján $$ \frac{\rd}{\rd t} \frac{\partial \mathcal{L}}{\partial \dot{y}} = \frac{\partial \mathcal{L}}{\partial y} = 0 $$ a hozzá tartozó $p_y = \partial_{\dot{y}}\mathcal{L}$ által definiált általános lendület időderiváltja nulla: ő egy megmaradó, lendület-szerű mennyiség.
3.1. példa: Csúszó ék - Tömegközéppont
Térjünk vissza ismét a csúszkáló alakzatokhoz, és használjuk ezt a példát egy általános trükk megismerésére. Ha nincsenek külső erők akkor a tömegközéppont gyorsulása nulla. Ebben a példában csak $y$ irányban hat külső erő (a gravitáció): jó ötlet lehet ezért az $x$ irányban megnézni egy tömegközéppont-szerű mennyiséget.
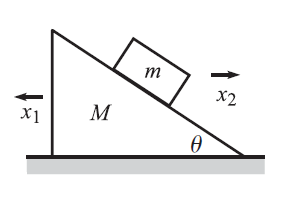
Legyenek az $x_1$ és $x_2$ helyett az új koordinátáink (emlékezve hogy a két $x$ koordinátát ellenkező előjellel vettük fel) $$ R = \frac{Mx_1-mx_2}{M+m} \quad \quad \text{és} \quad \quad r = x_1+x_2 $$ Térjünk át ezekre a koordinátákra, és vegyük figyelembe velük a kényszereket. Visszaidézve a kényszermentes Lagrange-ot: $$ \mathcal{L} = \frac{1}{2}M \dot{x_1}^2 + \frac{1}{2}M \dot{y_1}^2 + \frac{1}{2} m \dot{x_2}^2 + \frac{1}{2} m \dot{y_2}^2 +mgy_2 $$ A kényszereink most $y_1 = \text{konst.}$ és $y_2 = r \tan{\varphi}$ tehát a potenciál egyszerűen $$ V = -mg r \tan{\varphi} $$ ami már csak az egyik koordinátától függ.
A kinetikus tagban viszont történhetnek még csúnyaságok. Következő lépésként invertálnunk kell az új koordinátáink definícióját a régikre. Ez favágó módszerrel $$ \begin{aligned} x_1 &= r - x_2 \quad \quad \quad \quad \quad \quad x_2 = \frac{M}{m} x_1- \frac{M+m}{m}R \\ x_2 &= r - x_1 \quad \quad \quad \quad \quad \quad x_1 = \frac{m}{M} x_2+ \frac{M+m}{M}R \end{aligned} $$ egyenletrendszerre vezet, amik kicsit alakítva $$ \begin{aligned} x_1 = \frac{m}{M} (r-x_2)+ \frac{M+m}{M}R \quad \quad &\quad \quad \quad \quad x_2 = \frac{M}{m} (r-x_1)- \frac{M+m}{m}R \\ x_1 = \frac{m}{M+m} r+ R \quad \quad &\quad \quad \quad \quad x_2 = \frac{M}{M+m} r- R \end{aligned} $$ Egy fokkal haladóbb út az, ha ezt mátrixosan írjuk: $$ \begin{pmatrix} R \\ r \end{pmatrix} = \begin{pmatrix} \frac{M}{M+m} && -\frac{m}{M+m} \\ 1 && 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} $$ A fenti mátrixot invertálva (aminek részleteit később gyakoroljuk) $$ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 && \frac{m}{M+m} \\ -1 && \frac{M}{M+m} \end{pmatrix} \begin{pmatrix} R \\ r \end{pmatrix} $$ ugyanezt az eredményt kapjuk.
Minden esetre ezzel ki tudjuk fejezni a kinetikus tagunk $x$ komponenseit. Némi algebra után $$ \begin{aligned} M \dot{x_1}^2 + m \dot{x_2}^2 &= M\left( \frac{m}{M+m} \dot{r} + \dot{R} \right)^2 + m\left(\frac{M}{M+m}\dot{r} -\dot{R} \right)^2 \\ &=\frac{m^2M}{(M+m)^2} \dot{r}^2 +M \dot{R}^2 + 2\frac{mM}{M+m} \dot{r} \dot{R} + \frac{mM^2}{(M+m)^2}\dot{r}^2 +m\dot{R}^2 - 2 \frac{mM}{M+m} \dot{r} \dot{R} \\ &= m\frac{mM}{(M+m)^2} \dot{r}^2 + M\frac{mM}{(M+m)^2}\dot{r}^2 +(M+m)\dot{R}^2 \\ &= \frac{mM}{M+m} \dot{r}^2 +(M+m)\dot{R}^2 \end{aligned} $$ Bevezetve a $\mu$ redukált tömeget $$ \mu = \frac{mM}{M+m} $$ A teljes Lagrange-függvényünk $$ \mathcal{L} = \frac{1}{2}(M+m)\dot{R}^2 +\frac{1}{2} \mu \dot{r}^2 + \frac{1}{2} m \dot{r}^2 \tan^2{\varphi} + mg r \tan{\varphi} $$
Ebben már szépen látszik, hogy az $R$ koordináta sehol sem szerepel explicite: tehát a rá vonatkozó Euler-Lagrange egyenlet alapján $$ \begin{aligned} \ddot{R} &= 0 \\ M \ddot{x_1} - m \ddot{x_2} &= 0 \\ M \dot{x_1} - m \dot{x_2} &= \text{konst.} \end{aligned} $$ Tehát a tömegközéppont mozgásának $x$ komponense az, ami itt egy ciklikus koordináta. A hozzá tartozó lendület nem más, mint az $x$ irányú összlendület: ez egy megmaradó mennyiség. Mellesleg a másik, relatív koordinátára vonatkozó Euler-Lagrange eredménye $$ (\mu + m \tan^2{\varphi})\ddot{r} = mg \tan{\varphi} $$ visszaadja a múlt órán látott mozgásegyenletet. Eszerint a két test állandó $$ \ddot{r} = \frac{mg \tan{\varphi}}{\mu + m \tan^2{\varphi}} $$ gyorsulással távolodik egymástól az $x$ irányban. A múlt heti eredményeinket összeadva pontosan ezt a gyorsulást kapjuk, jópár algebrai lépés után amit most megspórolunk azzal, hogy elhisszük.
3.2. példa: Mozgás hengeren
Bár kétségtelenül ők a leggyakoribbak, nem csak Descartes-i és gömbi koordináták léteznek. Nézzünk most egy példát, ahol hengeres $(\rho, \varphi, z)$ koordinátázás lesz célravezető. Vegyünk egy $R$ sugarú, végtelenül magas hengert. Erre rögzítünk egy tömegpontot úgy, hogy csak a henger felületén mozoghat; majd bekapcsolunk egy erőt, ami az origó felé vonzza a tömegpontot, méghozzá $$ \vec{F} = -k \vec{r} $$ alakban. Mi lesz a pálya, ha elindítjuk a tömegpontot?
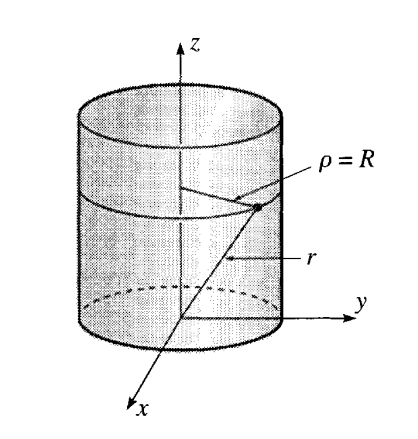
Először is: kellenek az energiák. A potenciál helyett itt most az erő van megadva, de ha még emlékszünk, hogy $$ \vec{F} = - \vec{\nabla} U $$ akkor visszakövetkeztethetünk rá, mint $$ U = \frac{1}{2} k \vec{r}^{\,2}= \frac{1}{2} k r^{2} $$ Itt $r$ a távolság az origótól: ő még nem hengeres. Kis Pitagorasz tétellel viszont $$ r^2 = z^2 + \rho^2 $$ tehát a potenciális tag hengerkoordinátákban: $$ U = \frac{1}{2} k (z^2 + \rho^2) $$ Ahova még beírhatjuk a $\rho = R$ kényszerünket: $$ U = \frac{1}{2} k (z^2 + R^2) $$
Kérdés még a kinetikus tag: milyen irányokban lehet sebessége a részecskének? A három hengeres irány közül csak $\rho$ nem játszhat, mert a felületre vagyunk korlátozva, így marad $z$ és $\varphi$. Hogy az utóbbiból sebességet csináljunk, meg kell javítani a dimenzióját egy hossz mértékegységű sugár szorzóval, ami itt $\rho = R$. $$ K = \frac{1}{2} m \dot{z}^2 + \frac{1}{2} m R^2 \dot{\varphi}^2 $$ A teljes Lagrange tehát: $$ \mathcal{L} = \frac{1}{2} m \dot{z}^2 + \frac{1}{2} m R^2 \dot{\varphi}^2 - \frac{1}{2} k (z^2 + R^2) $$ Ami két változótól függ: $z$ és $\varphi$. Mostmár felfegyverkezve viszont a ciklikus koordináták ismeretével, rögtön láthatjuk, hogy nincs explicit $\varphi$ függés benne, tehát $$ \frac{\partial \mathcal{L}}{\partial \varphi} = 0 $$ amiből következik, hogy $$ \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = mR^2 \dot{\varphi} = \text{konst.} $$ Ez egy megmaradó mennyiség, mint az előző példában az impulzus volt. Ahogy itt most $\varphi$ egy általános koordináta, a hozzá tartozó $mR^2 \dot{\varphi}$ mennyiség egy általános impulzus. Mivel ez a koordináta ciklikus (nincs explicit a Lagrange-ban), a hozzá tartozó általános impulzus megmarad. Kis átalakítással egyébként $$ p_\varphi = R \cdot m R \dot{\varphi} = R \cdot m v_\perp = R \cdot p_\perp = L $$ ez nem más mint a perdület.
Minden esetre, már az Euler-Lagrange felírása nélkül tudunk valamit a pályáról: a körkörös komponense a mozgásnak csupán egy állandó sebességű keringés lesz. Marad még a $z$ komponens, amire már kell az Euler-Lagrange: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial z} = -kz \qquad&\qquad\qquad \frac{\partial \mathcal{L}}{\partial \dot{z}} = m \dot{z} \\ m \ddot{z} &= - kz \\ \ddot{z} &= - \frac{k}{m} z = -\omega^2 z \end{aligned} $$ Ez szintén egy ismerős diffegyenlet lehet: a harmonikus oszcillátoré. Megoldása: $$ z(t) = A \cos{\left( \omega t + c \right)} $$ Összesítve a találtakat: a részecskénk körkörösen egyenletes sebességgel fog keringeni, míg a $z$ irányban fel-le oszcillál.
Noether-tétel
Megbarátkoztunk kicsit az általános impulzusokkal. Ezeket gyakran tudtuk összekötni egy vizuális megfigyeléssel a problémánkról: az $x$ tengelyen eltolható rendszereknél mindig megmarad az $x$ irányú lendület, a forgásszimmetrikus feladatokban pedig a perdület. Ezt a megfigyelést formalizálja, és általánosítja a Noether-tétel:
A Lagrange-függvény minden szimmetriájához tartozik egy megmaradó mennyiség.
Matematikailag ez azt jelenti, hogy a $q$ változóinkat eltranszformáljuk valahogy (pl. elforgatjuk) $$ \vec{q} \longrightarrow T (\vec{q}) \approx \vec{q} + \epsilon\, \vec{\varphi} $$ ami sorbafejthető az identitás transzformáció (ie.: nem csinálunk semmit, $\vec{q}\rightarrow \vec{q}$) körül. Ha erre a transzformációra változatlan a Lagrange függvényünk, akkor $$ P = \frac{\partial \mathcal{L}}{\partial \dot{\vec{q}}} \vec{\varphi} = \sum_i \frac{\partial \mathcal{L}}{\partial \dot{q_i}} \varphi_i = \vec{p} \vec{\varphi} $$ állandó. Nézzünk erre pár példát!
3.3. példa: 2D rugó
3.3.1. Descartes
Vegyünk egy egyszerű rugós testet egy síkban, és írjuk fel a Lagrange-át sima Descartes-i koordinátákban. Ahogy az előbb láthattuk, a rugó potenciális energiája $\frac{1}{2} k \vec{r}^{\,2}$, tehát $$ \mathcal{L} = \frac{1}{2} m (\dot{x}^2 + \dot{y}^2) - \frac{1}{2}k (x^2 + y^2) $$ Nézzük meg az $$ \begin{aligned} x \rightarrow x + \epsilon \, y \qquad\qquad\qquad y \rightarrow y - \epsilon \, x \end{aligned} $$ transzformációt, tehát ha $\vec{\varphi} = (y,\, -x)$! Ez mellesleg úgy is írható, mint $$ \begin{pmatrix} x \\ y \end{pmatrix} \longrightarrow \begin{pmatrix} 1 && \epsilon \\ -\epsilon && 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} $$ Ezt nézegetve kicsit, felismerhetjük hogy $\sin{\epsilon} \approx \epsilon$ és $\cos{\epsilon} \approx 1$, tehát ő nem más mint egy forgásmátrix közelítése.
Nézzük meg, hogy invariáns-e erre a transzformációra a Lagrange, kezdve a kinetikus taggal. Véve a deriváltakat: $$ \begin{aligned} \dot{x} \rightarrow \frac{\rd}{\rd t} (x + \epsilon \, y) = \dot{x} + \epsilon \dot{y} \qquad\qquad\qquad \dot{y} \rightarrow\frac{\rd}{\rd t} (y - \epsilon \, x) = \dot{y} - \epsilon \dot{x} \end{aligned} $$ amik négyzetei: $$ \begin{aligned} \dot{x}^2 \rightarrow \dot{x}^2 + 2 \epsilon \dot{x} \dot{y} + \underbrace{\epsilon^2 \dot{y}^2}_{\approx 0} \qquad\qquad\qquad \dot{y}^2 \rightarrow \dot{y}^2 - 2 \epsilon \dot{x} \dot{y} + \underbrace{\epsilon^2 \dot{x}^2}_{\approx 0} \end{aligned} $$ Tehát a kinetikus tag: $$ K \rightarrow \frac{1}{2}m (\dot{x}^2 + \dot{y}^2 + \underbrace{2 \epsilon \dot{x} \dot{y} - 2 \epsilon \dot{x} \dot{y}}_{=0}) = K $$ változatlan. Ugyanezt eljátszva a potenciális taggal: $$ V \rightarrow \frac{1}{2}k (x^2 + y^2 + + \underbrace{2 \epsilon x y - 2 \epsilon x y}_{=0}) = V $$ az is ugyanúgy néz ki, tehát ez egy szimmetria.
Ha már tujduk, hogy szimmetriáról beszélünk, nézzük meg mi marad meg a Noether-tétel szerint. Deriválva a Lagrange-ot a sebességek szerint megkapjuk az általános lendületeket: $$ \begin{aligned} p_x =\frac{\partial \mathcal{L}}{\partial \dot{x}} = m \dot{x} \qquad\qquad\qquad p_y=\frac{\partial \mathcal{L}}{\partial \dot{y}} = m \dot{y} \end{aligned} $$ amiket be kell szorozni még az infinitezimális $\varphi$ tagokkal: $$ \begin{aligned} P = \frac{\partial \mathcal{L}}{\partial \dot{x}} \varphi_x + \frac{\partial \mathcal{L}}{\partial \dot{y}} \varphi_y \\ = m \dot{x} \cdot y - m \dot{y} x \\ = p_x y - p_y x \end{aligned} $$ Ami nem más, mint a rendszer perdülete.
3.3.2. Polár
Írjuk most fel ugyanezt, csak polárkoordinátákban, a rugó végéből a testhez mutató $\vartheta$ szöggel és a rugó relatív megnyúlását leíró $R$ távolsággal. Ekkor a Lagrange $$ \mathcal{L} = \frac{1}{2} m (\dot{R}^2 + R^2 \dot{\vartheta}^2) - \frac{1}{2}k R^2 $$ Láthatjuk, hogy $\vartheta$ ciklikus, tehát az általános $p_\vartheta$ lendület megmarad, amiről már beláttuk korábban, hogy a perdület. Ez konzisztens az előző feladatrésszel, de gyakorlásképp nézzük meg mi lesz most az eltolás amire invariáns a Lagrange. A valóságban úgyis ez a nehezebb része a feladatoknak.
A változók transzformálása nem függ azok deriváltjaitól, ezért általában először a potenciális energiát érdemes nézegetni. Itt most ez teljesen független $\vartheta$-tól, tehát ott tetszőleges $$ \vec{\varphi} = \begin{pmatrix} 0 \\ \alpha \end{pmatrix} \quad \quad \text{azaz} \quad \quad R \rightarrow R+0, \quad \quad \vartheta \rightarrow \vartheta + \epsilon \alpha $$ transzformációk működnek. A kinetikus tagunkban viszont szerepel $\dot{\vartheta}$: hogy az változatlan maradjon, igaznak kell lennie $$ \dot{R}^2 + R^2 \dot{\vartheta}^2 = \dot{R}^2 + \dot{R}^2 (\dot{\vartheta}+\epsilon \dot{\alpha})^2 $$ összefüggésnek. Ezt kicsit kibontva: $$ \begin{aligned} \dot{R}^2 + R^2 \dot{\vartheta}^2 = \dot{R}^2 &+ \dot{R}^2 (\dot{\vartheta} ^2 +2\epsilon \dot{\vartheta} \dot{\alpha}) \\ \dot{\vartheta} \dot{\alpha} &= 0 \\ \dot{\alpha} &= 0 \end{aligned} $$ azt látjuk, hogy a szög transzformációja nem más, mint egy konstans eltolás. A hozzá tartozó megmaradó mennyiség pedig: $$ P = m R^2 \dot{\vartheta} \cdot \alpha $$ ismét a perdület, egy konstans $\alpha$ szorzó erejéig. Ezt bele lehet olvasztani az $\epsilon$-ba, és vehető egynek.
3.4. példa: Hengerben henger
Vegyünk egy $M$ tömegű, $R$ sugarú üres hengert. Rakjunk bele egy másik, $m$ tömegű $r$ sugarú hengert. A nagyot kezdjük el megforgatni valamilyen $\dot{\beta}$ sebességgel, a kicsit pedig hagyjuk csúszni: mi lesz ekkor a Lagrange, mik a szimmetriái és a megmaradó mennyiségei?
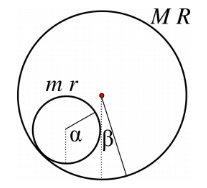
Nézzük meg először a feladat nehezét: a paraméterezést. Hol van a kis henger középpontja tetszőleges időpontban? Ehhez két dolgot kell tudnunk: a csúszásmentes mozgás feltételét, és egy kis geometriát. Utóbbihoz segít a lenti ábra.
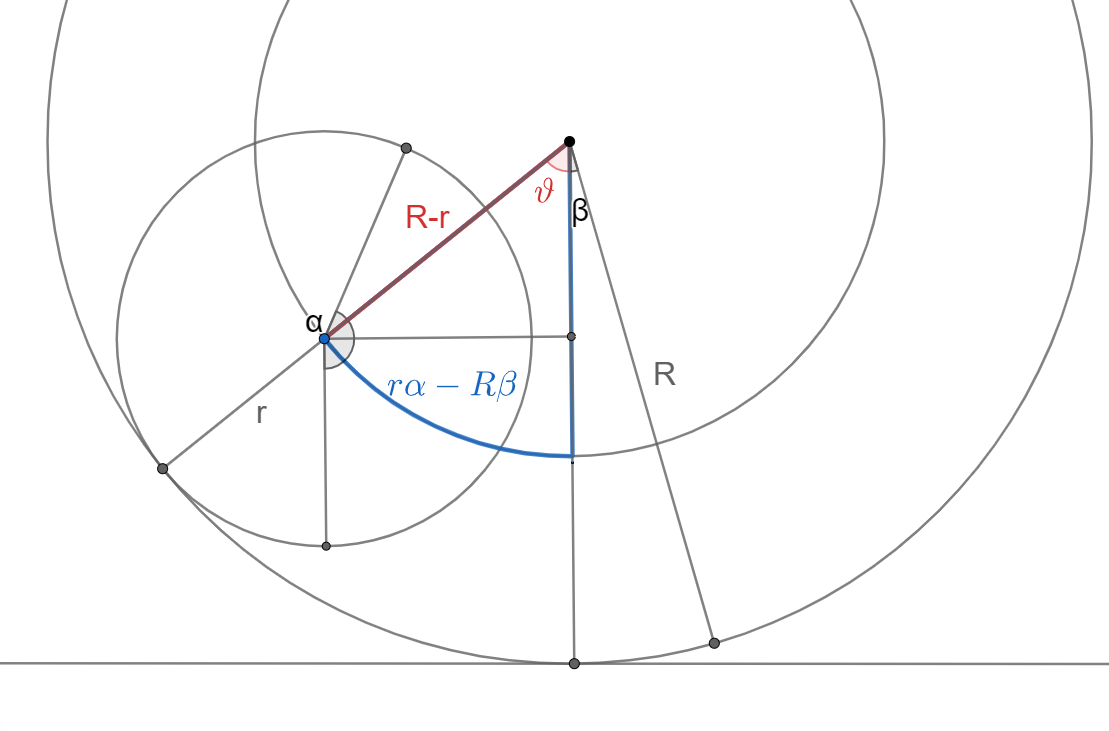
Ha csúszás nélkül történne a mozgás, akkor az érintkzési pontokban megegyeznének a kerületi sebességek, tehát $$ r \dot{\alpha_0} = R \dot{\beta_0} $$ És mivel nem lenne csúszás, a kis henger középpontja ott is maradna, ahol volt. Ha ez a feltétel viszont nem teljesül, akkor el fog mozdulni a kör körül, valamilyen $r \dot{\alpha} - R \dot{\beta}$ sebességgel. Ez alatt megtesz a kis henger középpontja valamennyi $\Delta l$ utat a nagy középpontja körül, méghozzá $$ \Delta l = r \alpha - R \beta $$ Tehát kis geometriával tetszőleges $(\alpha, \beta)$ változóknál a kis henger középpontjához kellő szög: $$ \vartheta = \frac{r \alpha - R \beta}{R-r} $$
Ezzel a kis kör középpontjának $(x_m, y_m)$ koordinátái: $$ \begin{aligned} x_m = (R-r) \sin{\frac{r \alpha - R \beta}{R-r}} \qquad\qquad\qquad y_m = (R-r) \cos{\frac{r \alpha - R \beta}{R-r}} \end{aligned} $$ Az utóbbival gyorsan fel is tudjuk írni a potenciális energiát, mint $$ V = -mg (R-r) \cos{\frac{r \alpha - R \beta}{R-r}} $$ A kis henger kinetikus energiájához nem elég tudni a középpontját: a kerületén lévő pontok szép gyorsan keringhetnek, szóval nekik is lesz kinetikus energiájuk. Egy tetszőleges pontja a kis körnek: $$ \begin{aligned} x = x_m + r \sin{\alpha} \qquad\qquad\qquad y &= y_m - r \cos{\alpha} \\ x = (R-r) \sin{\frac{r \alpha - R \beta}{R-r}} + r \sin{\alpha} \qquad\qquad\qquad y &= (R-r) \cos{\frac{r \alpha - R \beta}{R-r}} - r \cos{\alpha} \end{aligned} $$ Ezeket deriválva: $$ \begin{aligned} \dot{x} = \cos{\frac{r \alpha - R \beta}{R-r}} (r \dot{\alpha} - R \dot{\beta}) + r \dot{\alpha} \cos{\alpha} \qquad\qquad \dot{y} = -\sin{\frac{r \alpha - R \beta}{R-r}} (r \dot{\alpha} - R \dot{\beta}) + r \dot{\alpha} \sin{\alpha} \end{aligned} $$ Amiből a kinetikus tagba szükséges négyzetösszegük: $$ \begin{aligned} \dot{x}^2 + \dot{y}^2 &= r^2 \dot{\alpha}^2 + (r \dot{\alpha} - R \dot{\beta})^2 \\ \dot{x}^2 + \dot{y}^2 &= 2 r^2 \dot{\alpha}^2 + R^2 \dot{\beta}^2 - 2 r R \dot{\alpha} \dot{\beta} \end{aligned} $$ Tehát a kis henger kinetikus tagja: $$ K_m = m r^2 \dot{\alpha}^2 - m r R \dot{\alpha} \dot{\beta} + \frac{1}{2} m R^2 \dot{\beta}^2 $$ A nagy henger már egyszerűbb: az csak forog a tengelye körül, így $$ K_M = \frac{1}{2} M R^2 \dot{\beta}^2 $$ Tehát a teljes Lagrange: $$ \mathcal{L} = \frac{1}{2} M R^2 \dot{\beta}^2 + m r^2 \dot{\alpha}^2 - m r R \dot{\alpha} \dot{\beta} + \frac{1}{2} m R^2 +mg (R-r) \cos{\frac{r \alpha - R \beta}{R-r}} $$
Keressünk ebben valamilyen szimmetriát! Induljunk mi megint a potenciális energiából, azon belül is a $\cos$ tagból. Kis alakítással: $$ \cos{\frac{r \alpha - R \beta}{R-r}} = \cos{\left( r \frac{ \alpha - \frac{R}{r} \beta}{R-r}\right)} $$ Ez alapján tippeljük be a: $$ \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \longrightarrow \begin{pmatrix} \alpha \\ \beta \end{pmatrix} + \epsilon \begin{pmatrix} 1 \\ \frac{r}{R} \end{pmatrix} $$ alakú konstans transzformációt. Ezt nézegetve láthatjuk, hogy az $\alpha$ szöget, tehát a belső hengert elforgatjuk valamilyen $\epsilon$ szöggel; míg a külsőt a $\frac{r}{R} \epsilon$-al. Visszaidézve a csúszásmentes forgás feltételét, azt ez pont teljesíti.
Nézzük meg mi lesz a hozzá tartozó megmaradó mennyiség is. Véve az általános lendületeket: $$ \begin{aligned} p_\alpha &= \frac{\partial \mathcal{L}}{\partial \dot{\alpha}} = r^2 m\dot{\alpha} - mrR \dot{\beta} \\ p_\beta &= \frac{\partial \mathcal{L}}{\partial \dot{\beta}} = R^2 M \dot{\beta} - m r R \dot{\alpha} \end{aligned} $$ Majd megszorozva az infinitezimális trafókkal: $$ \begin{aligned} P &= (r^2 m\dot{\alpha} - mrR \dot{\beta}) + (R^2 M \dot{\beta} - m r R \dot{\alpha}) \frac{r}{R} \\ &= (r^2 m\dot{\alpha} - mrR \dot{\beta} + R r M \dot{\beta} - m r^2 \dot{\alpha}) \\ &= ( M-m) rR \dot{\beta} \end{aligned} $$ lesz a megmaradó mennyiségünk.
Közelítések
Gyakran előfordul, hogy a mozgásegyenletek amiket megkapunk nem oldhatók meg kézzel, vagy legalábbis nem könnyen. Ilyenkor nagyjából három lehetőség van:
- Numerikusan oldjuk meg őket, például python-ban a scipy csomaggal.
- Megnézzük a rendszer egyensúlyi pontjait, és azokról próbálunk meg valami okosat mondani.
- Addig közelítünk, amíg meg nem tudjuk oldani kézzel.
Most az utolsó ponttal fogunk foglalkozni. A közelítéseknek első lépése, hogy feltesszük egy változóról hogy pici, például $\varphi \ll 1$. Ekkor $\varphi$ összes függvényét ami megjelenik a problémánkban Taylor-sorba tudjuk fejteni a nulla körül tetszőleges rendig, ami gyakran már kezelhetőbb.
Emlékeztetőül tetszőleges $f(x)$ függvénynek az $a$ pont körüli Taylor sora: $$ f(x) \approx f(a) +\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2 + \mathcal{O}(x^3) $$ például $$ \begin{aligned} \sin{x} &\approx \sin{0}+\frac{\cos{0}}{1!}(x-0)+\frac{-\sin{0}}{2!}(x-0)^2 + \dots = x + \mathcal{O}(x^3) \\ \ln{(1+x)^2} &\approx \ln{(1+0)^2}+\frac{\frac{2(1+0)}{(1+0)^2}}{1!}(x-0) + \dots = 2x + \mathcal{O}(2) \end{aligned} $$ Őt hasznos gyakorolni, ha eddig lemaradt volna: az elemi függvények sorfejtését könnyű megkeresni, de az összetettekét már gyakran manuálisan kell kiszámolnunk.
3.5. példa: Inga
Bemelegítésként először írjuk fel a sima inga problémáját Lagrange-osan, polárkoordinátákkal. A kényszermentes Lagrange-függvény két tagja, ha origónak a felfüggesztési pontot vesszük: $$ \begin{aligned} K &= \frac{1}{2} m \dot{x}^2 + \frac{1}{2} m \dot{y}^2 \\ V &= mg (l-y) = -mgy + \textcolor{gray}{V_0} \end{aligned} $$ Ebbe jön majd a kényszerünk, miszerint $x^2 + y^2 = l^2$. Áttérve polárkoordinátákra $$ x = l \sin{\varphi} \quad \quad \text{és} \quad \quad y = l \cos{\varphi} $$ ez automatikusan teljesül, és a Lagrange-unk alakja $$ \mathcal{L} = \frac{1}{2} m l^2 \dot{\varphi}^2 + mgl \cos{\varphi} $$
A szükséges deriváltak $$ \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = ml^2 \dot{\varphi} \quad \quad \text{és} \quad \quad \frac{\partial \mathcal{L}}{\partial \varphi} = -mgl \sin{\varphi} $$ illetve $$ \frac{\rd}{\rd t }\frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = ml^2 \ddot{\varphi} $$ Amikből adódik a mozgásegyenlet: $$ \ddot{\varphi} = -\frac{g}{l} \sin{\varphi} $$ ami már ismerős lehet az előző óráról. Emlékeztetőül ott bevezettük $\omega = \sqrt{g/l}$-et, aztán kis szögekre közelítettünk mint $\varphi \ll 1$, amelynek eredményeképp $$ \ddot{\varphi} \approx -\omega^2 \varphi $$ egy harmonikus oszcillátort kapunk. Innen ered a közelítő eredmény az inga keringési idejére: $$ T \approx \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{l}{g}} $$
Ez mind szép és jó, viszont a közelítést már a mozgásegyenlet utolsó alakjában alkalmaztuk. Ez a precízebb és biztosabb mód: mégis kíváncsiak lehetünk, hogy lehet-e előbb. A válasz az, hogy igen, ha óvatosak vagyunk.
Kezdjük rögtön a Lagrange-al: $$ \mathcal{L} = \frac{1}{2} m l^2 \dot{\varphi}^2 \cdot 1 + mgl \cdot \cos{\varphi} $$ És közelítsünk a potenciális energiában másodrendig: $$ \mathcal{L} \approx \frac{1}{2} m l^2 \dot{\varphi}^2 \cdot 1 + mgl \cdot \left( 1 -\frac{\varphi^2}{2} \right) $$ Két tagot kaptunk: az első egy konstans, ami nem befolyásolja a fizikát, ezért lehagyható. A többi: $$ \mathcal{L} \approx \frac{1}{2} m l^2 \dot{\varphi}^2 \cdot 1 -\frac{1}{2} mgl \cdot\varphi^2 $$ Ebből kiszámolva a mozgásegyenletet, az eredmény $$ \ddot{\varphi} \approx - \omega^2 \varphi $$ pont ugyanaz, amit az előbb kaptunk.
3.6. példa: Rugós inga
Cseréljük le az előző feladat ingájának madzagát egy rugóra: mi lesz ekkor a mozgásegyenlet kis kitérésekre?
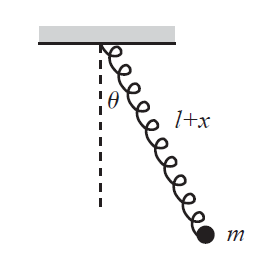
3.6.1. Általános megoldás
Ha belevesszük a rugót is: $$ V_{\text{rugó}} = \frac{1}{2} k \Delta l^2 $$ ahol $\Delta l$ fejezi ki, hogy mennyire nyúlt meg a rugó az eredeti $l_0$-hoz képest. Descartes-i koordinátákkal: $$ \begin{aligned} x^2 + y^2 &= l^2 = (l_0+\Delta l)^2 \\ \Delta l &= \sqrt{x^2 + y^2} - l_0 \end{aligned} $$
Hogy kiválasszuk a jó koordinátákat, gondolkodjunk kicsit a feladaton. Két dolgunk van: ingánk és rugónk. Az inga láttuk milyen jól illeszkedik a poláros koordinátázáshoz. A rugóban pedig az jelenik meg, hogy mennyit nyúl meg sugárirányban. Legyen a két változónk $\varphi$, az inga kitérési szöge, és $R$, az inga megnyúlása az eredeti $l_0$ hosszához képest. A régi változók nyelvén tehát: $$ \begin{aligned} x^2 + y^2 &= l^2 = (l_0 + R)^2 \\ x = l \sin{\varphi} &= (l_0 + R) \sin{\varphi} \\ y = l \cos{\varphi} &= (l_0 + R) \cos{\varphi} \end{aligned} $$ Milyen sebességek jelennek meg a kinetikus tagban? Lesz egyrészt a sugárirányú sebesség, ami azt mondja meg, hogy mennyire változik éppen $R$: $$ K_r = \frac{1}{2} m \dot{R}^2 $$ és lesz egy erre merőleges komponens, ami az érintő irányú sebesség lesz. Ez pedig a $\dot{\varphi}$ szögsebesség szorozva az $(l_0+R)$ sugárral, tehát $$ K_\varphi = \frac{1}{2} m (l_0+R)^2 \dot{\varphi}^2 $$ Ezeket összeadva pont ugyanazt kapjuk, mint amit a biztosabb behelyettesítéses módszerrel kaptunk volna.
A rugó potenciális energiája így már nagyon egyszerű: $$ V_{\text{rugó}} = \frac{1}{2} k R^2 $$ Cserébe a gravitációs potenciális energiánk lesz picit csúnyább: $$ V_{\text{grav.}} = mg (l_0+R) (1-\cos{\varphi}) $$ Ezzel kész is a Lagrange-unk: $$ \mathcal{L} = \frac{1}{2} m \dot{R}^2 + \frac{1}{2} m (l_0+R)^2 \dot{\varphi}^2 + mg (l_0+R) (\cos{\varphi}-1) - \frac{1}{2} k R^2 $$ és jöhetnek is az Euler-Lagrange egyenletek. Két változónk van, tehát kettő lesz: $$ \begin{aligned} &\frac{\partial \mathcal{L}}{\partial R} = m(l_0+R)\dot{\varphi}^2 + mg \cos{\varphi}-mg - kR \qquad\qquad \frac{\partial \mathcal{L}}{\partial \dot{R}} = m \dot{R} \\ &\frac{\partial \mathcal{L}}{\partial \varphi} = - mg (l_0+R) \sin{\varphi} \qquad\qquad\qquad\qquad\qquad\qquad \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = m(l_0+R)^2 \dot{\varphi} \end{aligned} $$ Amikkel elvégezve a deriválásokat: $$ \begin{aligned} (l_0+R)\dot{\varphi}^2 + g \cos{\varphi}-g - \frac{k}{m}R = &\ddot{R} \\ - g (l_0+R) \sin{\varphi} = 2(l_0+R)\dot{R} \dot{\varphi} + (l_0+R)^2 &\ddot{\varphi} \end{aligned} $$ Kicsit még szépítve: $$ \begin{aligned} \ddot{R} = &(l_0+R)\dot{\varphi}^2 + g (\cos{\varphi}-1) - \frac{k}{m}R \\ &(l_0+R) \ddot{\varphi} = - 2\dot{R} \dot{\varphi} - g \sin{\varphi} \end{aligned} $$ Ezt már be lehet küldeni a kedvenc numerikus megoldónknak, és meg is lesznek a pályák.
3.6.2. Közelítés
Arra vagyunk kíváncsiak, hogy kis kitérésekre mi lesz a megoldás. Ez itt két dolgot jelent: a szög is kicsit tér ki az egyensúlyi helyzetéből, és a rugó is. Tehát $$ \varphi \ll 1 \quad \quad \text{és} \quad \quad R \ll l_0 $$ Ha még nem megy magabiztosan a közelítés, akkor csináljuk a következőt: legyen $$ \varphi = \varepsilon\varphi_0 \quad \quad \text{és} \quad \quad R = \varepsilon R_0 $$ ami dimenziósan korrekt. Ezt beírva a mozgásegyenleteinkbe, illetve a szögfüggvényeket Taylor-sorba fejtve: $$ \begin{aligned} \varepsilon\ddot{R_0} = (l_0+\varepsilon R_0)\varepsilon^2 \dot{\varphi_0}^2 +g-g - \frac{k}{m} \varepsilon R_0 \\ (l_0+\varepsilon R_0) \varepsilon\ddot{\varphi_0} = - 2\varepsilon^2\dot{R_0} \dot{\varphi_0} - g \varepsilon\varphi_0 \end{aligned} $$ Ki tudjuk kukázni az $\epsilon$-ban elsőrenden túlmenő tagokat: $$ \begin{aligned} \varepsilon\ddot{R_0} \approx - \frac{k}{m} \varepsilon R_0 \\ (l_0) \varepsilon\ddot{\varphi_0} \approx - g \varepsilon\varphi_0 \end{aligned} $$ Tehát $$ \begin{aligned} \ddot{R_0} \approx - \frac{k}{m} R_0 \\ \ddot{\varphi_0} \approx - \frac{g}{l_0} \varphi_0 \end{aligned} $$ első rendben a megoldásaink szeparálódnak két független harmonikus oszcillátorra: az egyik frekvenciája a szokásos rugóé, a másiké pedig az ingáé.
Ha rögtön a Lagrange-ban közelítenénk, akkor az már bonyolultabb egy csatolt rendszer esetén. A potenciális energiában ugyanúgy lehet másodrendben közelíteni: $$ \begin{aligned} V_{\text{grav.}} &= mg (l_0+R) (1-\cos{\varphi}) \approx mg (l_0+R) \left(1-1+\frac{\varphi^2}{2}\right) \\ &\approx \frac{1}{2} mg l_0 \varphi^2 \end{aligned} $$ A kinetikus tagban figyelnünk kell, hogy összességében a koordináták és a sebességek rendje is egyezzen ezzel. Van például az a tagunk, hogy $$ \frac{1}{2} m (l_0+R)^2 \dot{\varphi}^2 $$ ami összességében másodrendű kell, hogy legyen. Mivel $\dot{\varphi}^2$ rendjét nem tudjuk csökkenteni, ezért a másik tag csak nulladik rendig számít. Ergo $\frac{1}{2}m l_0^2 \dot{\varphi}^2$ lesz. Az összesített közelítő Lagrange-unk tehát $$ \mathcal{L} \approx \frac{1}{2} m \dot{R}^2 + \frac{1}{2} m l_0 \dot{\varphi}^2 -\frac{1}{2} m g l_0 \varphi^2 - \frac{1}{2} k R^2 $$ nem más, mint két egymással nem kommunikáló oszcillátor, ahogy fentebb is beláttuk.
Kis megjegyzés a beadandóhoz és a további feladatokhoz: ha például egy olyan kinetikus tagunk van, hogy $$ K \propto \left(\dot{x_1} \cos{x_1} + \dot{x_2} \sin{x_2}+\dot{x_1}\frac{\ln{(x_2)}}{x_2}\right)^2 $$ akkor is figyelni kell a sorfejtés rendjére. Itt például ha minden koordinátának a függvényét elsőrendig fejtjük (nulla körül $\cos{x}\approx1$, $\sin{x}\approx x$, $\ln{(1+x)}\approx x$) akkor $$ K \approx \left(\dot{x_1} + \dot{x_2} x_2+\dot{x_1}\right)^2 $$ és látszik, hogy egyetlen olyan tagunk lesz csak, ami összességében másodrendű: $$ K \approx 4 \dot{x_1}^2 + \mathcal{O}(x^3) $$
3.7. példa: Éken csúszó inga
Múlt héten említettem, hogy a Lagrange-i mechanika feladatok olyanok mint a LEGO: csak össze kell rakni az őket felépítő blokkokat, aztán szisztematikusan megy a megoldás. Most nézzük meg ezt pár eddigi példa darabjaiból. Vegyünk egy asztalhoz rögzített háromszög alakú éket, amire rakjunk egy $M$ tömegű téglatestet, ami rajta szabadon, súrlódásmentesen mozoghat. Rakjunk erre a téglatestre egy $l$ hosszúságú ingát, egy $m$ tömegű testtel a végén. Mi lesz az inga mozgásegyenlete?
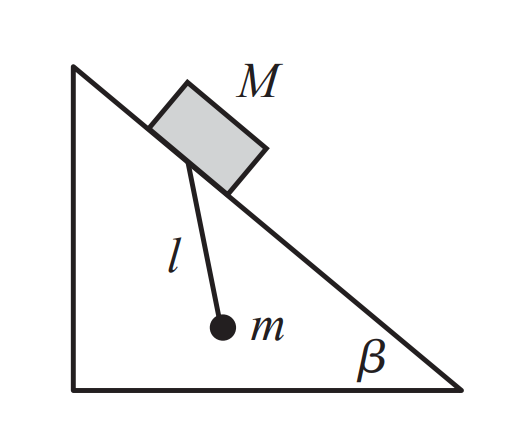
Keressük meg a jó változókat! Ezek tipikusan olyanok, amik automatikusan teljesítik a kényszereket a Lagrange-ban: például azt, hogy a téglatest az éllel párhuzamosan mozog. Legyen ennek a koordinátája $z$. Az inga pedig adja magát egy $\varphi$ szöghöz, amit a felfüggesztésétől nézünk. A kinetikus energia ekkor: $$ K = \frac{1}{2} M \dot{z}^2 + \frac{1}{2} m l^2 \dot{\varphi}^2 + K_{m,k} $$ Ahol $K_{m,k}$ az ingán lógó test kinetikus tagja a lecsúszásból adódóan. Mielőtt őt kiszámítjuk, nézzük meg a potenciális energiát. Az sajnos már nem illeszkedik olyan szépen a koordinátákhoz: a két test magassága kell hozzá. Ez a téglatestre $$ \begin{aligned} \frac{y}{z} = \sin{\beta} \qquad\qquad \text{tehát} \qquad\qquad y = z \sin{\beta} \end{aligned} $$ Az ingán lógó test pedig még ez alatt fog lógni, hozzá képest egy extra $l \cos{\varphi}$ távolságot. Ezzel a potenciális energia $$ V = - Mgz \sin{\beta} - mg \left( z \sin{\beta} + l \cos{\varphi}\right) $$
A hiányzó kinetikus tagunkhoz fel tudjuk használni az itt kifejezett $y_m$ távolságot, és a hasonló $x$ irányú eltérülését is az ingának: $$ \begin{aligned} x_m &= z \cos{\beta} + l \sin{\varphi} \\ \dot{x_m} &= \dot{z}\cos{\beta} + l \dot{\varphi} \cos{\varphi} \end{aligned} $$ Hasonlóképpen az $y_m$ tagra: $$ \dot{y_m} = -\dot{z}\sin{\beta} + l \dot{\varphi} \sin{\varphi} $$ A kettő négyzetösszege pedig: $$ \dot{x_m}^2 + \dot{y_m}^2 = \dot{z}^2 + l^2 \dot{\varphi} ^2 + 2 l \dot{\varphi}\dot{z} (\cos{\beta}\cos{\varphi} - \sin{\beta} \sin{\varphi}) $$ Ahol megtaláljuk a már betippelt tagokat, illetve azt ami hiányzott: $$ K_{m,k} = 2 l \dot{\varphi}\dot{z} (\cos{\beta}\cos{\varphi} - \sin{\beta} \sin{\varphi}) = 2 l \dot{\varphi}\dot{z} \cos{(\varphi+\beta)} $$
Ezzel együtt tehát a teljes Lagrange: $$ \mathcal{L} = \frac{1}{2} M \dot{z}^2 + \frac{1}{2} m l^2 \dot{\varphi}^2 + ml \dot{\varphi}\dot{z} \cos{(\varphi+\beta)} + Mgz \sin{\beta} + mg \left( z \sin{\beta} + l \cos{\varphi}\right) $$ A mozgásegyenletek pedig, a téglatesttel kezdve: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial z} = (M+m) g \sin{\beta} \qquad\qquad\qquad \frac{\partial \mathcal{L}}{\partial \dot{z}} = M \dot{z} + m l\dot{\varphi} \cos{(\varphi+\beta)} \end{aligned} $$ $$ \begin{aligned} (M+m) g \sin{\beta} = M \ddot{z} + ml\ddot{\varphi}\cos{(\varphi+\beta)} -ml \dot{\varphi}^2 \sin{(\varphi+\beta)} \end{aligned} $$ Az ingára pedig: $$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial \varphi} = - ml \dot{\varphi}\dot{z} \sin{(\varphi+\beta)} - mgl \sin{\varphi} \qquad\qquad \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = m l^2 \dot{\varphi} + ml \dot{z} \cos{(\varphi+\beta)} \end{aligned} $$ $$ \begin{aligned} - ml \dot{\varphi}\dot{z} \sin{(\varphi+\beta)} - mgl \sin{\varphi} &= m l^2 \ddot{\varphi} + ml \ddot{z} \cos{(\varphi+\beta)} - ml \dot{z} \dot{\varphi} \sin{(\varphi+\beta)} \\ - mgl \sin{\varphi} &= m l^2 \ddot{\varphi} + ml \ddot{z} \cos{(\varphi+\beta)} \\ l \ddot{\varphi} &= - g \sin{\varphi} - \ddot{z} \cos{(\varphi+\beta)} \end{aligned} $$
Mit kapunk akkor, ha mind $\varphi$ mind $\beta$ kicsit? Ekkor $$ \begin{aligned} (M+m) g \beta &= M \ddot{z} + ml\ddot{\varphi} \\ l \ddot{\varphi} &= - g \varphi - \ddot{z} \end{aligned} $$ kis rendezéssel $$ \begin{aligned} (M+m) g \beta &= -M l \ddot{\varphi}-Mg \varphi + ml\ddot{\varphi} \\ (m-M)l\ddot{\varphi} &= (M+m) g \beta + Mg \varphi \end{aligned} $$ Csináljunk egy kis változócserét! Legyen $$ u = \varphi + \frac{M+m}{M} \beta $$ ezt megszorozva $Mg$-vel: $$ Mgu = Mg\varphi + g(M+m) \beta $$ ami pont az egyenletünk jobb oldala. A változót deriválva pedig azt tapasztaljuk, hogy $\ddot{u} = \ddot{\varphi}$ tehát azt az egyenletet is megoldhatnánk, hogy $$ \begin{aligned} (m-M)l\ddot{u} = Mgu \\ \ddot{u} = -\frac{M}{M-m} \frac{g}{l} u \end{aligned} $$ Ez nem más, mint egy harmonikus oszcillátor (megint). Kis szöges közelítésben tehát az inga harmonikusan rezeg, csak egy picit eltolva: függőleges helyett attól $\frac{M+m}{M} \beta $ szöggel eltolva.