Elmecha
4. óra Letöltés
Kisrezgések, normálmódusok
Bár a mozgásegyenleteket könnyen fel tudjuk írni a Lagrange-i mechanika módszereivel, láthattuk, hogy azokat megoldani már általánosan nem mindig lehet. Van viszont egy nevezetes rendszer amit jól ismerünk és szeretünk: a harmonikus oszcillátor. Ha egy adott rendszert valamilyen közelítésben (pl. kis szögek) át tudunk alakítani valami oszcillátor-szerűvé (rezgések) akkor vissza tudjuk vezetni a problémát valami jól megoldhatóra.
Emlékeztetőül egy darab egy dimenziós harmonikus oszcillátor Lagrange-függvénye (valamilyen általános $q$ koordinátával): $$ \mathcal{L} = \frac{1}{2} m \dot{q}^2 - \frac{1}{2}k q^2 $$ amit kicsit másképp is írhatunk: $$ \mathcal{L} = \frac{1}{2} \dot{q}m \dot{q} - \frac{1}{2}q k q $$ Ha több, akár egymással kölcsönható rugónk is van, akkor is ilyen alakú lesz a megoldás. Viszont több koordináta esetén $q$ helyett $\underline{q}$ vektoraink lesznek, a Lagrange viszont egy skalár mennyiség. Ahhoz hogy skalárt kapjunk vektorokból, a tippelt alak a több rugós Lagrange-ra: $$ \mathcal{L} = \frac{1}{2} \dot{\underline{q}}^T \underline{\underline{M}}\ \dot{\underline{q}} - \frac{1}{2} \underline{q}^T \underline{\underline{D}}\, \underline{q} $$ tehát sorvektor, mátrix, oszlopvektor alakú tagjaink kell hogy legyenek.
Ennek az alaknak van egy nagy előnye: ismerősen néz ki, és az Euler-Lagrange egyenlet is teljesen hasonló egy harmonikus oszcillátoréra: $$ \begin{aligned} \frac{\rd }{\rd t} \frac{\partial \mathcal{L}}{\partial {\dot{\underline{q}}}} &= \frac{\partial \mathcal{L}}{\partial {\underline{q}}} \\ \underline{\underline{M}}\, \ddot{\underline{q}} &=- \underline{\underline{D}}\, \underline{q} \\ \ddot{\underline{q}} &= -\underline{\underline{M}}^{-1}\underline{\underline{D}}\, \underline{q} \\ \ddot{\underline{q}} &= -\underline{\underline{A}}\, \underline{q} \end{aligned} $$ végeredményéül pedig ilyen alakú mozgásegyenletet kapunk. Ha itt nem vektorok lennének, akkor ez egy szögfüggvény diffegyenlete lenne: mivel több dimenzióban vagyunk, jó ötlet az, ha a megoldást szögfüggvények lineárkombinációjaként keressük, valamilyen $$ \underline{q} = \sum_i c_i \underline{\eta}^i \cos{\left( \omega_i t + \delta_i\right)} $$ alakban. Az állítás az, hogy ezek az $\underline{\eta}$ vektorok (amikből kikombinálható a tényleges megoldás) sajátvektorai az $\underline{\underline{A}}$ mátrixnak: őket hívjuk normálmódusoknak. A szögfüggvényekben megjelenő $\omega$ frekvenciák pedig a hozzájuk tartozó sajátfrekvenciák.
Ez így még egész száraznak tűnhet: pár példa után megbarátkozunk vele. A lényeges lépések minden esetre:
- Felírjuk mátrixosan a Lagrange függvényt (akár közelítésekkel).
- Kiszámoljuk az $\underline{\underline{A}} = \underline{\underline{M}}^{-1}\underline{\underline{D}}$ mátrixot (ez egy invertálás aztán egy mátrixszorzás).
- Megkeressük a sajátrendszerét, amiből adódnak a megoldásaink.
4.1. példa: Csúszkáló inga
Vegyünk egy $M$ tömegű testet, és rögzítsük egy sínre a gravitációval merőlegesen. Erre akasszunk egy $l$ hosszúságú ingát, rajta egy $m$ tömeggel. Milyen mozgást végez a rendszer kis kitérések esetén?
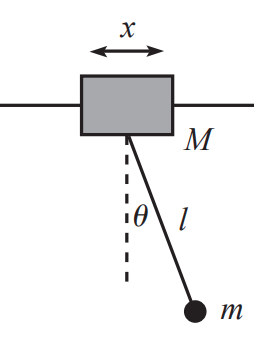
Nézzük meg ezt a példát két féle megoldáson keresztül. Minden esetre a kiindulási pont a Lagrange-lesz, amit írjunk fel az egyensúlyi helyzettől vett eltérésekkel. Ez a példa egyszerű: ránézésre akkor van egyensúlyban a rendszer, ha $x=0$ és $\vartheta = 0$: ezek már magukban jó általános koordináták. Kiindulásul a Descartes-i Lagrange: $$ \mathcal{L} = \frac{1}{2} M \dot{x}^2 + \frac{1}{2} M \dot{y}^2 + \frac{1}{2} m \left( \dot{x_m}^2 + \dot{y_m}^2 \right) - mg y_m $$ Amire még ki kell róni a kényszereinket. Egyrészt a test a sínen mozog, tehát $\dot{y} = \text{konst.}$, másrészt pedig az inga hossza fix: ezt már láttuk, a polárkoordináták teljesítik automatikusan.
A kis tömegpont koordinátái $$ \vec{r}_m = \vec{r}_M + \begin{pmatrix} l \sin{\varphi} \\ -l \cos{\varphi} \end{pmatrix} =\begin{pmatrix} x \\ 0 \end{pmatrix} +\begin{pmatrix} l \sin{\varphi} \\ -l \cos{\varphi} \end{pmatrix} $$ tehát kis matekkal $$ \mathcal{L} = \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left( \dot{x}^2 + l^2\dot{\vartheta}^2 + 2 l \dot{x}\dot{\vartheta} \cos{\vartheta}\right) + mgl \cos{\vartheta} $$ Ebből a Lagrange-ból kell megmondanunk a mozgást. Először nézzünk meg egy speciálisabb utat ami általában nem működik, de ennél a feladatnál egyszerűbb lesz miatta az életünk. Aztán a megoldás tudatában váltsunk át a szisztematikus, mindig működő módszerekre.
4.1.1. Lendületmegmaradás
Vegyük észre, hogy $x$ ciklikus: tehát $p_x$ megmarad. Ezért $$ p_x = \frac{\partial \mathcal{L}}{\partial \dot{x}} = M\dot{x} + m\dot{x} + ml\dot{\vartheta}\cos{\vartheta} = \text{konst.} $$ Hogyha csak a kis szögekre vagyunk kíváncsiak, akkor első rendben $$ \begin{aligned} \dot{x}&(m+M) + ml\dot{\vartheta} = A^\prime \\ \dot{x}&= - \frac{ml}{m+M }\dot{\vartheta} + A \\ \int \dot{x} \rd t&= - \int \frac{ml}{m+M }\dot{\vartheta} \rd t + \int A \rd t \\ x(t) &= - \frac{ml}{m+M } \vartheta + At + B \end{aligned} $$
Ami marad még, az a másik változó Euler-Lagrange egyenlete: $$\begin{aligned} \frac{\partial \mathcal{L}}{\partial \vartheta} = - ml \dot{x}\dot{\vartheta} \sin{\vartheta} - mgl \sin{\vartheta} \qquad\qquad \frac{\partial \mathcal{L}}{\partial \dot{\vartheta}} = m l^2 \dot{\vartheta} + ml \dot{x} \cos{\vartheta} \end{aligned}$$ $$ m l^2 \ddot{\vartheta} + ml \ddot{x} \cos{\vartheta} -m l \dot{x} \dot{\vartheta} \sin{\vartheta} = - ml \dot{x}\dot{\vartheta} \sin{\vartheta} - mgl \sin{\vartheta} $$ Amire alkalmazzuk a is szöges közelítést, és egyszerűsítsünk. A közelítésben most első rendig megyünk el, mert a nem-szögfüggvényeket tartalmazó $ml^2 \ddot{\vartheta}$ tag elsőrendű a szögben: a többit is célszerű eddig közelíteni. $$ \ddot{\vartheta} + \frac{1}{l} \ddot{x} = - \frac{g}{l} \vartheta $$ Ebbe be tudjuk írni $x(t)$-t a lendületmegmaradásból kiszámított időfüggéssel: $$ \begin{aligned} \ddot{\vartheta} - \frac{m}{m+M } &\ddot{\vartheta} = - \frac{g}{l} \vartheta \\ \left(1 - \frac{m}{m+M }\right) &\ddot{\vartheta} = - \frac{g}{l} \vartheta \\ &\ddot{\vartheta} = - \frac{g}{l} \frac{m+M}{M} \vartheta \end{aligned} $$
Ez egy ismerős differenciálegyenlet: a szögfüggvények második deriváltja pont egy negatív előjellel arányos saját magukkal. Keressük tehát a megoldást $$ \vartheta(t) = C \cos{\left(\omega t + \delta \right)} $$ alakban. Ezt visszaírva $$ - C \omega^2 \cos{\left(\omega t + \delta \right)} = - \frac{g}{l} \frac{m+M}{M} \vartheta $$ tehát megoldja a tippelt függvényünk a mozgásegyenletet, ha $$ \omega^2 = \frac{g}{l} \frac{m+M}{M} $$
Összegezve, a megoldásunk a két változóra: $$ \begin{aligned} \vartheta (t) &= C \cos{\left(\omega t + \delta \right)} \\ x(t) &= - C \frac{ml}{m+M } \cos{\left(\omega t + \delta \right)}+ At + B \end{aligned} $$ Ami azt mutatja, hogy az inga oszcillál, az őt tartó test mozgása pedig egy azonos frekvenciájú oszcillációból és egy $x$ irányú egyenletes mozgásból áll.
4.1.2. Általános megoldás
A fenti megoldás működött, de kihasználta a lendület megmaradását: sajnos ezt nem mindig tudjuk megtenni. Hogy a bonyolultabb feladatok megoldásához szükséges mátrixos írásmódot gyakoroljuk, alkalmazzuk azt is erre a feladatra.
Először is, fel kell írnunk a Lagrange-ot mátrixosan az általános koordinátákkal, $$ \mathcal{L} = \frac{1}{2} \dot{\underline{q}} \underline{\underline{M}} \dot{\underline{q}} - \frac{1}{2} \underline{q} \underline{\underline{D}} \underline{q} $$ alakban. Na ez így még nem fog menni a mi Lagrangunkra, szóval közelítsünk most rögtön a Lagrange-ban. Menjünk el a szögben másodfokig: így a deriválások után elsőfokú tagok lesznek a mozgásegyenletben. Ebben a közelítésben $\cos{\vartheta} \approx 1 - \frac{\vartheta^2}{2}$, tehát $$ \mathcal{L} = \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left( \dot{x}^2 + l^2\dot{\vartheta}^2 + 2 l \dot{x}\dot{\vartheta} - \underbrace{l \dot{x}\dot{\vartheta}\vartheta^2} \right) + \underbrace{mgl }- \frac{1}{2}mgl\vartheta^2 $$ Itt két tagot is elhagyhatunk: az első aláhúzott már harmadfokú, a második pedig egy konstans. Ez már felírható szépen, mint $$ \mathcal{L} = \frac{1}{2} \begin{pmatrix} \dot{x} \\ \dot{\vartheta} \end{pmatrix} \begin{pmatrix} M+m && ml \\ ml && ml^2 \end{pmatrix} \begin{pmatrix} \dot{x} \\ \dot{\vartheta} \end{pmatrix} - \frac{1}{2} \begin{pmatrix} x \\ \vartheta \end{pmatrix} \begin{pmatrix} 0 && 0 \\ 0 && mgl \end{pmatrix} \begin{pmatrix} x \\ \vartheta \end{pmatrix} $$ Elvégezve a mátrixos alakra a deriválgatást, az Euler-Lagrange $$ \begin{aligned} \underline{\underline{M}} \ddot{\underline{q}} &= - \underline{\underline{D}} \underline{q} \\ \ddot{\underline{q}} &= - \underline{\underline{M}}^{-1} \underline{\underline{D}} \underline{q} \end{aligned} $$ Keressük a $\underline{q}$ megoldását valamilyen tippelt próbafüggvények lineáris kombinációjaként: $$ \underline{q} = \sum_i c_i \underline{\eta}_i \cos{\left(\omega_i t + \delta_i \right)} $$
Hogy megtaláljuk ezeket az $\underline{\eta}$ vektorokat és $\omega$ frekvenciákat, meg kell oldanunk az $ \underline{\underline{A}} = \underline{\underline{M}}^{-1} \underline{\underline{D}}$ mátrix sajátproblémáját. Először kell a tömegmátrix inverze, ami két dimenzióban egyszerűbb: $$ \underline{\underline{M}}^{-1} = \frac{1}{\det{\underline{\underline{M}}}} \text{adj}\underline{\underline{M}} $$ a determinánsból és a (mátrix értelemben vett) adjungált mátrixból tevődik össze. Tehát nekünk $$ \begin{aligned} \underline{\underline{M}}^{-1} &= \frac{1}{m(m+M)l^2-m^2l^2} \begin{pmatrix} ml^2 && -ml \\ -ml && M+m \end{pmatrix} \\ \underline{\underline{M}}^{-1} &= \frac{1}{Mml^2} \begin{pmatrix} ml^2 && -ml \\ -ml && M+m \end{pmatrix} \end{aligned} $$ Marad a mátrixszorzás, ami most relatíve gyorsan megvan: $$ \underline{\underline{A}} = \frac{1}{Mml^2} \begin{pmatrix} 0 && -m^2l^2g \\ 0 && (M+m)mgl \end{pmatrix} = \begin{pmatrix} 0 && -\frac{m}{M}g \\ 0 && \frac{M+m}{M}\frac{g}{l} \end{pmatrix} $$ Ennek a sajátértékeit jelöljük $\omega^2$-el. A rájuk vonatkozó sajátértékegyenlet pedig a spuros-determinánsos képletből $$ - \omega^2 \left( \frac{M+m}{M}\frac{g}{l} - \omega^2 \right) = 0 $$
Ennek két megoldása van: egyrészt lehet $\omega_0 = 0$. Másrészt lehet $$ \omega^2 =\frac{M+m}{M}\frac{g}{l} $$ Nézzük meg a hozzájuk tartozó sajátvektorokat! Az első esetben $$ \begin{pmatrix} 0-0 && -\frac{m}{M}g \\ 0 && \frac{M+m}{M}\frac{g}{l} - 0 \end{pmatrix} \underline{\eta_0} = \mathbf{0} $$ Ennek normált megoldása: $$ \underline{\eta_0} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$ Van tehát egy komponensünk, ami az $x$ irányban $\omega_0=0$ frekvenciával oszcillál: ez nem egy rezgés, tehát a módszertanunk nem alkalmas a tárgyalására. Egyébként ő az, ami egy egyenletes eltolásként és sebességként jelenik meg a megoldásban.
A másik sajátértékre $$ \begin{pmatrix} -\frac{M+m}{M}\frac{g}{l} && -\frac{m}{M}g \\ 0 && 0 \end{pmatrix} \underline{\eta} = \mathbf{0} $$ amit megold $$ \underline{\eta} = \begin{pmatrix} - \frac{m l }{m+M} \\ 1 \end{pmatrix} $$ Ez a szög irányában egy $\omega$ frekvenciás oszcilláció, ami az $x$ irányra egy $- \frac{m l }{m+M}$ faktorral terjed át. A mozgásegyenletek megoldása tehát ebben a formalizmusban: $$ \begin{pmatrix} x \\ \vartheta \end{pmatrix} = C \begin{pmatrix} - \frac{m l }{m+M} \\ 1 \end{pmatrix} \cos{\left(\omega t + \delta \right)} + B \begin{pmatrix} 1 \\ 0 \end{pmatrix} \cos{\left(0 t + \delta_0 \right)} $$ Ez szépen visszaadja a "rendes" megoldásunk oszcilláló részét: láthatjuk viszont, hogy az egyenes mozgás kiesett.
4.2. példa: Rudas inga
Vegyünk egy $l$ hosszúságú ingát, aminek a végére rögzítsünk egy $M$ tömegpontot. Ezen a ponton fűzzünk át az ingára merőlegesen egy sínt: erre pedig rakjunk egy $m$ tömegű testet. Mik a normálmódusok?
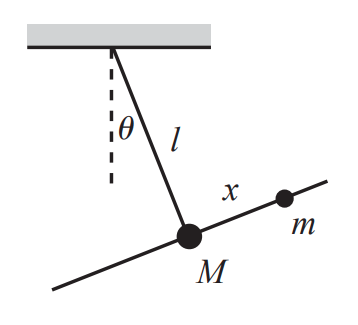
Tippeljük meg ismét a jó általános koordinátákat: ha a tömegek egybeesnek, és az inga pont lefelé mutat, egyensúlyban vagyunk. Legyenek az ettől való eltérés általános koordinátái $\varphi$ és $r$. Az $M$ tömegpont Descartes-i koordinátái (a potenciál nullpontjához illeszkedve): $$ \begin{aligned} \begin{pmatrix} x_M \\ y_M \end{pmatrix} = \begin{pmatrix} l \sin{\varphi} \\ -l \cos{\varphi} \end{pmatrix} \end{aligned} $$ A kis tömegpont már bonyolultabb: ahhoz kell a rúd és a horizont közötti szög. Kis geometriával belátható, hogy az is $\varphi$. Ezzel $$ \begin{pmatrix} x_m \\ y_m \end{pmatrix} = \begin{pmatrix} x_M \\ y_M \end{pmatrix} + \begin{pmatrix} r \cos{\varphi} \\ r\sin{\varphi} \end{pmatrix} $$ Deriválva: $$ \begin{pmatrix} \dot{x_M} \\ \dot{y_M} \end{pmatrix} = \begin{pmatrix} l \dot{\varphi} \cos{\varphi} \\ l \dot{\varphi} \sin{\varphi} \end{pmatrix} $$ $$ \begin{pmatrix} \dot{x_m} \\ \dot{y_m} \end{pmatrix} = \begin{pmatrix} l \dot{\varphi} \cos{\varphi} - r \dot{\varphi} \sin{\varphi} + \dot{r} \cos{\varphi} \\ l \dot{\varphi} \sin{\varphi} - r \dot{\varphi}\cos{\varphi} -\dot{r}\sin{\varphi} \end{pmatrix} $$
Emeljük ezeket négyzetre: $$ \dot{x_M}^2 + \dot{y_M}^2 = l^2 \dot{\varphi}^2 $$ $$ \begin{aligned} \dot{x_m}^2 =((l\dot{\varphi}+\dot{r})\cos{\varphi}-r\dot{\varphi}\sin{\varphi})^2 \qquad \qquad \dot{y_m}^2 =((l\dot{\varphi}-\dot{r})\sin{\varphi}-r\dot{\varphi}\cos{\varphi})^2 \\ \dot{x_m}^2 =(l\dot{\varphi}+\dot{r})^2\cos^2{\varphi}+r^2\dot{\varphi}^2\sin^2{\varphi}-2(l\dot{\varphi}+\dot{r})r\dot{\varphi}\cos{\varphi}\sin{\varphi} \\ \dot{y_m}^2 = (l\dot{\varphi}-\dot{r})^2\sin^2{\varphi}+r^2\dot{\varphi}^2\cos^2{\varphi}-2(l\dot{\varphi}-\dot{r})r\dot{\varphi}\cos{\varphi}\sin{\varphi} \end{aligned} $$ Összeadva a komponenseket $$\begin{aligned} &\dot{x_m}^2+ \dot{y_m}^2 = (l\dot{\varphi}+\dot{r})^2\cos^2{\varphi} + (l\dot{\varphi}-\dot{r})^2\sin^2{\varphi} + +r^2\dot{\varphi}^2\sin^2{\varphi}+r^2\dot{\varphi}^2\cos^2{\varphi} -2(l\dot{\varphi}+\dot{r})r\dot{\varphi}\cos{\varphi}\sin{\varphi} -2(l\dot{\varphi}-\dot{r})r\dot{\varphi}\cos{\varphi}\sin{\varphi} \\ &\dot{x_m}^2+ \dot{y_m}^2 = (l^2\dot{\varphi}^2+\dot{r}^2 + 2 l\dot{\varphi}\dot{r})\cos^2{\varphi} + (l^2\dot{\varphi}^2+\dot{r}^2 - 2 l\dot{\varphi}\dot{r})\sin^2{\varphi} + r^2\dot{\varphi}^2 -4rl\dot{\varphi}^2\cos{\varphi}\sin{\varphi}\\ &\dot{x_m}^2+ \dot{y_m}^2 = (l^2\dot{\varphi}^2+\dot{r}^2)\cos^2{\varphi} + 2 l\dot{\varphi}\dot{r}\cos^2{\varphi} +(l^2\dot{\varphi}^2+\dot{r}^2)\sin^2{\varphi} - 2 l\dot{\varphi}\dot{r}\sin^2{\varphi} +r^2\dot{\varphi}^2 -4rl\dot{\varphi}^2\cos{\varphi}\sin{\varphi}\\ &\dot{x_m}^2+ \dot{y_m}^2 = 2 l\dot{\varphi}\dot{r}(\cos^2{\varphi} - \sin^2{\varphi}) +l^2\dot{\varphi}^2+\dot{r}^2 +r^2\dot{\varphi}^2 -4rl\dot{\varphi}^2\cos{\varphi}\sin{\varphi} \\ &\dot{x_m}^2+ \dot{y_m}^2 = 2 l\dot{\varphi}\dot{r}(1 - 2\sin^2{\varphi}) +l^2\dot{\varphi}^2+\dot{r}^2 +r^2\dot{\varphi}^2 -4rl\dot{\varphi}^2\cos{\varphi}\sin{\varphi} \\ &\dot{x_m}^2+ \dot{y_m}^2 = 2 l\dot{\varphi}\dot{r} +l^2\dot{\varphi}^2+\dot{r}^2 +r^2\dot{\varphi}^2 -4rl\dot{\varphi}^2\cos{\varphi}\sin{\varphi} -4 l\dot{\varphi}\dot{r} \sin^2{\varphi} \end{aligned}$$ Amikkel a kinetikus tagok nagyjából készen is vannak. A potenciális: $$ V = - Mg l\cos{\varphi} - mg (l\cos{\varphi}-r\sin{\varphi}) $$ Ha rezgésekre vagyunk kíváncsiak, megint át kell írni az ebből kapott Lagrange-függvényt valamilyen közelítésekkel. A kis szög itt is működik, egy pontig: $$\begin{aligned} \dot{x_m}^2+ \dot{y_m}^2 \approx 2 l \dot{\varphi}\dot{r} +l^2 \dot{\varphi}^2 +\dot{r}^2 +r^2\dot{\varphi}^2 -4lr\dot{\varphi}^2\varphi -4 l\dot{\varphi}\dot{r}\varphi^2 \end{aligned}$$ Viszont két változónk van: $x$-re is ki kell szabnunk valamit, ha benne is kicsik a rezgések. Praktikai szempontból pedig az a célunk, hogy mátrixosan tudjuk felírni a kinetikus tagot, tehát a tagjainkban csak $\dot{r}$ és $\dot{\varphi}$ szerepeljenek (szigorúan másodrendben), maguk a változók ne. Ezt a két problémát egy csapásra tudjuk megoldani, ha feltesszük hogy $r \ll l$ tehát $\frac{r}{l}\ll 1$. Ekkor megjelölve, hogy mi hányadrendű a kis változókban: $$\begin{aligned} \dot{x_m}^2+ \dot{y_m}^2 \approx 2 l^2 \underbrace{\dot{\varphi}\frac{\dot{r}}{l}}_{\mathcal{O}(2)} +l^2 \underbrace{\dot{\varphi}^2}_{\mathcal{O}(2)} +l^2 \underbrace{\frac{\dot{r}^2}{l^2}}_{\mathcal{O}(2)} +l^2\underbrace{\frac{r^2}{l^2}\dot{\varphi}^2}_{\mathcal{O}(4)} -4l^2 \underbrace{\frac{r}{l}\dot{\varphi}^2\varphi}_{\mathcal{O}(4)} -4 l^2\underbrace{\dot{\varphi}\frac{\dot{r}}{l}\varphi^2}_{\mathcal{O}(4)} \end{aligned}$$ láthatjuk, hogy csak az első három tag kell nekünk: egyrészt a többi már negyedrendű, másrészt pont ők azok, amik felírhatók mátrixosan. A teljesség jegyében még nézzük meg a potenciált is: $$\begin{aligned} V \approx -\underbrace{ Mg l}_{\mathcal{O}(0)} + \frac{Mg l}{2}\underbrace{\varphi^2}_{\mathcal{O}(2)} - \underbrace{mgl}_{\mathcal{O}(0)} + \frac{mgl}{2} \underbrace{\varphi^2}_{\mathcal{O}(2)}+mgl \underbrace{\frac{r}{l}\varphi}_{\mathcal{O}(2)} \end{aligned}$$
Így a Lagrange: $$ \mathcal{L} = \frac{1}{2} \dot{\underline{q}} \underline{\underline{M}} \dot{\underline{q}} - \frac{1}{2} \underline{q}\underline{\underline{D}} \underline{q} $$ ahol $$ \begin{aligned} \underline{\underline{M}} = \begin{pmatrix} m && ml \\ ml && l^2(M+m) \end{pmatrix} \qquad\qquad \underline{\underline{D}} = \begin{pmatrix} 0 && mg \\ mg && (m+M)lg \end{pmatrix} \end{aligned} $$ A normálmódusok megtalálásához ismét számítsuk ki az $\underline{\underline{A}} = \underline{\underline{M}}^{-1}\underline{\underline{D}}$ mátrixot! Ehhez $$ \underline{\underline{M}}^{-1} = \frac{1}{m l^2(M+m)-m^2l^2}\begin{pmatrix} l^2(M+m) && -ml \\ -ml && m \end{pmatrix} = \frac{1}{M l} \begin{pmatrix} l\frac{M+m}{m} && -1 \\ -1 && \frac{1}{l} \end{pmatrix} $$ Amivel $$ \underline{\underline{A}} = \frac{1}{M l} \begin{pmatrix} l\frac{M+m}{m} && -1 \\ -1 && \frac{1}{l} \end{pmatrix} mg \begin{pmatrix} 0 && 1 \\ 1 && \frac{m+M}{m}l \end{pmatrix} = \frac{m}{M} \frac{g}{l}\begin{pmatrix} -1 && 0 \\ \frac{1}{l} && \frac{M}{m} \end{pmatrix} $$ Amiből a sajátértékek egyenlete: $$ \omega^4 - \frac{g}{l}\left(\frac{M-m}{M}\right)\omega^2 - \frac{m}{M}\left(\frac{g}{l}\right)^2= 0 $$ Most rábízva a szimbolikus programokra a megoldást, azok $$ \omega_1^2 = \frac{g}{l} \qquad \qquad \omega_2^2 = - \frac{m}{M}\frac{g}{l} $$ A normálmódusok pedig (normálás nélkül): $$\begin{aligned} \eta_1 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \qquad \qquad \eta_2 = \begin{pmatrix} -l \frac{m+M}{m} \\ 1 \end{pmatrix} \end{aligned}$$
Gerjesztések
A harmonikus mozgásokkal már jól megbarátkoztunk. Ezeknek eggyel bonyolultabb esete, ha vesszük az eddigi rezgő rendszerünket, és rákapcsolunk valami külső erőt. Arra vagyunk kíváncsiak, hogy mi lesz ekkor a mozgás, feltéve, hogy a külső erő nélküli rendszert már ismerjük. Egy matekos ismétlésként nézzük a következő differenciálegyenletet: $$ (\partial_t^2 + \omega_0^2) x(t) = f(t) $$ és gyorsan vegyük át a lépéseket a megoldásához.
Először is: ez bonyolult. Oldjuk meg először $x$ helyett valami $G$ függvényre abban az eseten, ha a jobb oldalt szereplő erő csak egy Dirac-delta. $$ (\partial_t^2 + \omega_0^2) G(t) = \delta(t) $$ Ő azért jó nekünk, mert az ismeretében tetszőleges $f(t)$ erőre meg tudjuk mondani a megoldást: $$ x(t) = \int_{-\infty}^\infty G(t- t^\prime) f(t^\prime) \rd t^\prime $$ Ezt ha behelyettesítjük az eredeti egyenletbe, akkor láthatjuk, hogy megoldja azt. Minden esetre még csak alrébbtoltuk a problémát: most $x$ helyett a $G$ Green-függvényt kell megtalálnunk. Ez kinézhető táblázatokból, például a harmonikus oszcillátor rendszerére: $$ G(t) =\Theta(t) \frac{\sin{(\omega_0 t)}}{\omega_0} $$ amivel tetszőleges gerjesztőerőre fel tudjuk írni a megoldást, a fenti integrállal.
Persze minket most a mátrixos jelölés érdekel. Ekkor a mozgásegyenletünk igazából $$ \underline{\underline{M}} \ddot{\underline{q}} + \underline{\underline{D}} \underline{q} = \underline{F} $$ Ezt kicsit alakítva $$ \ddot{\underline{q}} +\underline{\underline{M}}^{-1} \underline{\underline{D}} \underline{q} = \underline{\underline{M}}^{-1} \underline{F} $$ Hasonlóan a fentihez, ennek általános megoldása helyett először nézzük a $$ (\partial_t^2 + \underline{\underline{M}}^{-1}\underline{\underline{D}}) \hat{G}(t) = \delta(t) $$ egyenletet. A sima oszcillátor megoldásából idézzük vissza, hogy megtaláltuk $\underline{\underline{M}}^{-1}\underline{\underline{D}}$ sajátrendszerét: ezek voltak a normálmódusok, amikre $$ (\underline{\underline{M}}^{-1}\underline{\underline{D}}) \underline{\eta_i} = \omega_i^2 \underline{\eta_i} $$ A sajátvektorok diadikus szorzatát felhasználva pedig felírhatunk két fontos mátrixot velük: $$\begin{aligned} \underline{I} = \sum_i\underline{\eta_i} \underline{\tilde{\eta_i}} && \underline{\underline{M}}^{-1}\underline{\underline{D}} =\sum_i \omega_i^2 \underline{\eta_i} \underline{\tilde{\eta_i}} \end{aligned}$$ Ahol megjelenik $\underline{\tilde{\eta_i}}$, a sajátvektorhoz tartozó duális, amire $\underline{\tilde{\eta_i}} \underline{{\eta_j}} = \delta_{ij}$. Ha a sajátrendszer teljes és ortogonális, őt vehetjük egyszerűen a vektor transzponáltjának. Minden esetre ezzel a lépéssel rögzítettük a bázisunkat a sajátrendszerhez, amit tartsunk fejben. Ha visszaírunk mindent, és addig hunyorítunk hogy ne lássunk vektorokat, akkor ez úgy néz ki mint a sima oszcillátor, tehát $$ "\hat{G}(t) \propto - \sum_i \frac{\sin{(\omega_i t)}}{\omega_i} " $$ kinézetű megoldást keresünk, a vektoros-mátrixos részen kívül.
A mátrixos részhez emlékezzünk vissza, hogy a Green függvény $$ \int \hat{G}(t- t^\prime) \underline{\underline{M}}^{-1} \underline{F} $$ alakban szerepel nekünk a megoldásban: hatni fog valamilyen vektorra. Ha mi eddig a sajátbázisban dolgoztunk, akkor ezt az $M^{-1}F$ vektort is át kell rá transzformálni. Így a helyes mátrixos alakba bekerül még az $M^{-1}F$ vektor átírása is erre a bázisra (meg persze egy $\Theta$ lépcsőfüggvény): $$ \hat{G}(t) = \underline{\underline{G}}(t) = \Theta(t) \sum_i \frac{\sin{(\omega_i t)}}{\omega_i} \underline{\eta_i}\underline{\tilde{\eta_i}} $$ Kicsit nézegetve ez két dolgot csinál. Először is, hattatva a gerjesztő erőre, azt levetíti valamelyik sajátmódus irányába. Ebben az irányban pontosan úgy hat, mint a sima oszcillátorra a gerjesztés. Ezeket összegezve az összes módusra, megkapjuk a teljes hatását a forrástagnak. Mindez persze szép bonyolultan hangzik, szóval nézzünk is rá pár példát!
4.3. példa: Szinuszos gerjesztés harmonikus oszcillátorra
Bemelegítésként nézzünk meg egy sima harmonikus oszcillátort, amire rákapcsolunk egy $\Omega$ frekvenciájú, $f_0$ amplitúdójú szinuszos gerjesztést a $t=0$ pillanattól kezdve: $$ \begin{aligned} (\partial_t^2 + \omega_0^2) x &= f(t) \\ f(t) &= f_0 \sin{(\Omega t)} \Theta(t) \end{aligned} $$ Itt a gerjesztőerőben a $\Theta(t)$ lépcsőfüggvény a "$t=0$ pillanattól kezdve" szófordulat átfogalmazása matekra.
Tudjuk, hogy a Green függvény ismeretében a megoldás $$ x(t) = \int_{-\infty}^\infty G(t-t^\prime) f(t^\prime) \rd t^\prime $$ és hogy a sima oszcillátorra $$ G(t) = \Theta(t) \frac{\sin{\omega t}}{\omega} $$ Mivel a forrásmentes rendszer egy sima harmonikus oszcillátor, amit ismerünk, nincs más dolgunk, mint beírni ezeket az integrálba, ügyelve, hogy minek mi az argumentuma: $$ x(t) = \int_{-\infty}^\infty \Theta(t-t^\prime) \frac{\sin{\omega (t-t^\prime)}}{\omega} f_0 \sin{(\Omega t^\prime)} \Theta(t^\prime) \rd t^\prime $$ Nézzük meg mit csinálnak ezek a lépcsőfüggvények. A $\Theta(t^\prime)$ annyit tud, hogy $t^\prime = 0$ alatt nulla, felette pedig egy. Ezzel be van szorozva az integrandus: tehát annyit tesz, mintha $-\infty$ helyett 0-tól integrálnánk. A másik, $\Theta(t-t^\prime)$ akkor lesz nulla, ha $t-t^\prime < 0$, tehát ha $t^\prime > t$. Ez egy felső korlátot ad az integrálunknak $t$-nél. Ezeket beírva, illetve kiemelve mindent ami konstans: $$ x(t) = \frac{f_0}{\omega}\int_{0}^t \sin{[\omega (t-t^\prime)]}\sin{(\Omega t^\prime)} \rd t^\prime $$
Nézzük meg hogyan kell elvégezni egy ilyen integrált kézzel, papíron. Először is, trigonometriából tudjuk, hogy $$ \begin{aligned} \cos(x+y) &= \cos{x} \cos{y} - \sin{x} \sin{y} \\ \cos(x-y) &= \cos{x} \cos{y} + \sin{x} \sin{y} \end{aligned} $$ Az alsóból kivonva a fölsőt: $$ \begin{aligned} \cos(x-y) - \cos(x+y) = 2 \sin{x} \sin{y} \end{aligned} $$ Tehát nekünk: $$ \sin{[\omega (t-t^\prime)]}\sin{(\Omega t^\prime)} = \frac{\cos{[\omega (t-t^\prime) - \Omega t^\prime]} - \cos{[\omega (t-t^\prime) + \Omega t^\prime]}}{2} $$ Amivel az integrálunk két rész összegéből fog állni: $$ \frac{1}{2} \int_0^t \cos{[\omega (t-t^\prime) - \Omega t^\prime]} \rd t^\prime - \frac{1}{2} \int_0^t \cos{[\omega (t-t^\prime) + \Omega t^\prime]} \rd t^\prime $$
Nézzük most csak az elsőt, és vezessünk be egy $u$ változócserét: $$ \begin{aligned} u &= \omega (t-t^\prime) - \Omega t^\prime \\ \frac{\rd u}{ \rd t^\prime} &= -\omega - \Omega = -(\Omega + \omega) \end{aligned} $$ Tehát az integrál: $$ \int_0^t \cos{[\omega (t-t^\prime) - \Omega t^\prime]} \rd t^\prime = - \frac{1}{\Omega + \omega} \int \cos{u} \rd u $$ Amire kell még figyelnünk, azok a határok. Ezek rendre: $$ \begin{aligned} u(t^\prime=0) = \omega t \qquad\qquad u(t^\prime = t) = - \Omega t \end{aligned} $$ ahol feltűnhet, hogy a fenti határ igazából lentebb van, mint a lenti. Ezeket felcserélhetjük, ami hoz egy negatív szorzót az integrál elé, így: $$ - \frac{1}{\Omega + \omega} \int \cos{u} \rd u = \frac{1}{\Omega + \omega} \int_{-\Omega t}^{\omega t} \cos{u} \rd u $$ Ezt már egyszerű kiintegrálni: $$ \begin{aligned} \frac{1}{\Omega + \omega} \int_{-\Omega t}^{\omega t} \cos{u} \rd u &= \frac{1}{\Omega + \omega} \left[\sin{\omega t} - \sin{(-\Omega t)} \right] \\ &= \frac{1}{\Omega + \omega} \left[\sin{\omega t} + \sin{\Omega t} \right] \end{aligned} $$
A másik integrálunk is hasonló lesz, annyi különbséggel, hogy ott $$ \begin{aligned} w &= \omega (t-t^\prime) + \Omega t^\prime \\ \frac{\rd w}{ \rd t^\prime} &= -\omega + \Omega = \Omega - \omega \end{aligned} $$ illetve $$ \begin{aligned} w(t^\prime=0) = \omega t \qquad\qquad w(t^\prime = t) = \Omega t \end{aligned} $$ Tehát ez az integrál: $$ \begin{aligned} \int_0^t \cos{[\omega (t-t^\prime) + \Omega t^\prime]} \rd t^\prime &= \frac{1}{\Omega - \omega} \int_{\omega t}^{\Omega t} \cos{w} \rd w \\ &= \frac{1}{\Omega - \omega} \left[\sin{\Omega t} - \sin{\omega t} \right] \end{aligned} $$ Véve a kettő különbségét, közös nevezőre tudunk hozni: $$ \begin{aligned} &\frac{1}{\Omega + \omega} \left[\sin{\omega t} + \sin{\Omega t} \right] - \frac{1}{\Omega - \omega} \left[\sin{\Omega t} - \sin{\omega t} \right] = \\ = &\frac{(\Omega - \omega) \sin{\omega t} +(\Omega - \omega)\sin{\Omega t} - (\Omega + \omega) \sin{\Omega t} + (\Omega + \omega) \sin{\omega t} }{(\Omega + \omega) (\Omega - \omega)} \\ = &\frac{2 \Omega \sin{\omega t} - 2 \omega \sin{\Omega t} }{\Omega^2 - \omega^2} \end{aligned} $$
Visszaírva minden elhagyott szorzó faktort, ezzel a megoldásunk: $$ x(t) = \frac{f_0}{\omega} \frac{ \Omega \sin{\omega t} - \omega \sin{\Omega t} }{\Omega^2 - \omega^2} $$ Így megkaptuk egzakt formában a kitérés-idő függvényt. Vele már tudunk számolni bármit, ami érdekelhet a mozgásról. Most például nézzük meg, hogy hol lesz a kitérés nulla, tehát $$ x(t_0) = 0 $$ Ehhez $$ \begin{aligned} \frac{f_0}{\omega} &\frac{ \Omega \sin{\omega t_0} - \omega \sin{\Omega t_0} }{\Omega^2 - \omega^2} = 0 \\ &\Omega \sin{\omega t_0} - \omega \sin{\Omega t_0} = 0 \\ &\Omega \sin{\omega t_0} = \omega \sin{\Omega t_0} \\ &\ \,\frac{\sin{\omega t_0}}{\sin{\Omega t_0}} = \frac{\omega}{\Omega} \end{aligned} $$ Vegyük azt a speciális esetet, ahol $\Omega = 2 \omega$. Ekkor $$\begin{aligned} \frac{\sin{\omega t_0}}{\sin{(2 \omega t_0)}} = \frac{1}{2} \end{aligned}$$ Egy addíciós tétel után $$ \sin{2x} = 2 \sin{x} \cos{x} $$ tehát $$\begin{aligned} \frac{\sin{\omega t_0}}{2\sin{\omega t_0} \cos{\omega t_0}} = \frac{1}{2} \\ \frac{1}{\cos{\omega t_0}} = 1 \end{aligned}$$ Ami teljesül, ha $$\begin{aligned} \omega t_0 = 2 k \pi && k \in \mathbb{Z} \end{aligned}$$
4.4. példa: Tripla rugós kéttest rendszer
Most nézzünk valami tényleges fizikai rendszert ami nem csak közelítve lesz oszcillátor: két különböző $m_1$, $m_2$ tömegű golyót, amiket kössön össze egymással egy $K$ állandójú rugó; illetve a hozzájuk közelebbi falakkal 1-1 rendre $k_1$ és $k_2$ állandójú rugó.
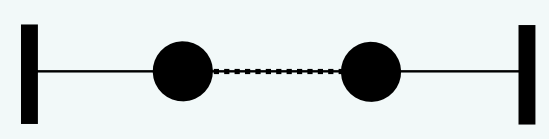
Legyenek az általános koordinátáink az egyensúlyi helyzettől való eltérést leírő $q_1$ és $q_2$. Ekkor a Lagrange: $$ \mathcal{L} = \frac{1}{2} m_1 \dot{q_1}^2 + \frac{1}{2} m_2 \dot{q_2}^2 - \frac{1}{2} k_1 q_1^2 - \frac{1}{2} k_2 q_2^2 - \frac{1}{2} K (q_2 - q_1)^2 $$ Ezt mátrixossá alakíthatjuk: $$ \mathcal{L} = \frac{1}{2} \begin{pmatrix} \dot{q_1} \\ \dot{q_2} \end{pmatrix}^T \underbrace{\begin{pmatrix} m_1 && 0 \\ 0 && m_2 \end{pmatrix}}_{= M} \begin{pmatrix} \dot{q_1} \\ \dot{q_2} \end{pmatrix} - \frac{1}{2} \begin{pmatrix} q_1 \\ q_2 \end{pmatrix}^T \underbrace{ \begin{pmatrix} k_1 + K && -K \\ -K && k_2 + K \end{pmatrix}}_{=D} \begin{pmatrix} q_1 \\ q_2 \end{pmatrix} $$ Visszaidézve még a sima rugóknál használt $\omega^2 = \frac{k}{m}$ frekvenciát, dimenziótlanítani is tudjuk a mátrixokat, majd megoldani a sajátérték-problémát. $$\begin{aligned} A = \underbrace{\begin{pmatrix} 1/m_1 && 0 \\ 0 && 1/m_2 \end{pmatrix}}_{= M^{-1}}\begin{pmatrix} k_1 + K && -K \\ -K && k_2 + K \end{pmatrix} = \begin{pmatrix} \frac{k_1 + K}{m_1} && -\frac{K}{m_1} \\ -\frac{K}{m_2} && \frac{k_2 + K}{m_2} \end{pmatrix} \end{aligned}$$
Legyen $\omega_1^2 = \frac{k_1}{m_1}$, $\omega_2^2 = \frac{k_2}{m_2}$, $\alpha = \frac{K}{k_1}$ és $\beta = \frac{K}{k_2}$, amikkel $$ A = \begin{pmatrix} w_1^2 (1+\alpha) && -w_1^2 \alpha \\ -\omega_2^2 \beta && w_2^2(1+\beta) \end{pmatrix} $$ Végül, ha bevezetjük még $\gamma = \frac{\omega_2^2}{\omega_1^2}$-et: $$ A = w_1^2\begin{pmatrix} 1+\alpha && - \alpha \\ -\gamma \beta && \gamma(1+\beta) \end{pmatrix} $$ Az általános megoldáshoz ennek kellene megoldani a sajátérték-problémáját.
4.5. példa: Háromrugós rendszer gerjesztése
Nézzük meg az előző rendszert, csak kicsit leegyszerűsítve az elrendezést, hogy tükörszimmetrikus legyen. Hattassuk erre egy erőt a következő alakban: $$ f(t) = \frac{f_0}{\tau} \Theta(t) \Theta(\tau-t) $$ Tehát egy konstans erő a $t\in [0,\tau]$ időintervallumban, azon kívül pedig nulla. Diskutáljuk, hogy mi történik annak függvényében, hogy melyik testre hatunk vele.
4.5.1. Sajátmódusok
Legyen most szimmetrikus a rendszer, tehát $m_1 = m_2$ és $k_1 = k_2$ ≠ $K$. Emlékeztetőül, ekkor a mátrixaink: $$\begin{aligned} \underline{\underline{M}} = \begin{pmatrix} m && 0 \\ 0 && m \end{pmatrix} \qquad\qquad \underline{\underline{D}} = \begin{pmatrix} k+K && -K \\ -K && k+K \end{pmatrix} \end{aligned}$$ amivel egyszerűen $$ \underline{\underline{A}} = \frac{1}{m}\underline{\underline{D}} $$ A sajátértékekre ekkor: $$ \left( \frac{k+K}{m} - \omega^2\right)^2 - \frac{K^2}{m^2} = 0 $$ Legyen a lustaság kedvéért $\omega_0^2 = k/m$ és $\Omega_0^2 = K/m$, így $$\begin{aligned} &\left( \Omega_0^2+\omega_0^2 - \omega^2\right)^2 - \Omega_0^4= 0 \\ \omega^4 - &2(\Omega_0^2+\omega_0^2) \omega^2 + (\Omega_0^2+\omega_0^2)^2 - \Omega_0^4 = 0 \\ \omega^2 = &\Omega_0^2+\omega_0^2 \pm \sqrt{(\Omega_0^2+\omega_0^2)^2 - (\Omega_0^2+\omega_0^2)^2 + \Omega_0^4} \end{aligned}$$ $$\begin{aligned} \omega_1^2 =\omega_0^2 && \omega_2^2 =\omega_0^2 + 2\Omega_0^2 \end{aligned}$$
Az ezekhez tartozó sajátmódusok pedig, mivel $$ A = \begin{pmatrix} \omega_0^2+\Omega_0^2 && -\Omega_0^2 \\ -\Omega_0^2 && \omega_0^2+\Omega_0^2 \end{pmatrix} $$ innen kis matekkal $$\begin{aligned} \underline{\eta_1} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix} \qquad\qquad \underline{\eta_2} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \end{pmatrix} \end{aligned}$$ Ezek ugyebár két harmonikus mozgást írnak le: az elsőnél a két test azonos irányba mozdul ki, a másiknál pedig ellentétesbe. Ezekhez a módusokhoz kell illesztenünk a gerjesztésünket. Tehát a Green függvényünk komponensei a sajátmódusok rendszerén, kihasználva, hogy most teljes ortonormált: $$ \left(\frac{1}{\Theta(t) } \cdot\right)\underline{\underline{G}}(t) = \sum_i \frac{\sin{(\omega_i t)}}{\omega_i} \underline{\eta}\underline{\tilde{\eta}} = \frac{\sin{(\omega_1 t)}}{\omega_1} \underline{\eta_1}\underline{\eta_1}^T + \frac{\sin{(\omega_2 t)}}{\omega_2} \underline{\eta_2}\underline{\eta_2}^T $$ Ha ezt hattatjuk a gerjesztő erőnkre, akkor az $\underline{\eta}\underline{\eta}^T$ tagok gyakorlatilag egy projektorfelbontást fognak rajta végezni: fel kell írnunk a forrástagunkat ezekkel a vektorokkal.
4.5.2. Azonos lökés
Ha mindkét testet azonos erővel lökdössük, akkor ezen a bázison az erő: $$\begin{aligned} \underline{\underline{M}}^{-1}\underline{F} = \frac{F(t)}{m} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + 0 \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} \qquad\qquad F(t) = \frac{f_0}{\tau} \Theta(t)\Theta(\tau-t) \end{aligned}$$ Tehát a koordináták időfejlődése: $$ \underline{q} = \int_{-\infty}^\infty \Theta(t^\prime) \Theta(\tau-t^\prime) \Theta (t-t^\prime) \frac{f_0}{m \tau} \frac{\sin{(\omega_1 (t-t^\prime))}}{\omega_1} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} \rd t^\prime $$
Vegyük azt az esetet, ahol $t>\tau$, és nézzük meg mi történik a lépcsőfüggvényekkel. A $\Theta(t^\prime)$ a lenti határt fogja megadni, hiszen $-\infty$ és $0$ közt nullával szoroz mindent. A másik kettő a felső határt: az egyik $t$ a másik $\tau$ felett szoroz mindent nullával. Mivel itt $\tau$ a kisebb, ő lesz a felső határunk: $$ \underline{q} = \int_{0}^\tau \frac{f_0}{m \tau} \frac{\sin{(\omega_1 (t-t^\prime))}}{\omega_1} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} \rd t^\prime $$ Az integrálás után: $$ \underline{q} = \frac{f_0}{m \tau \omega_0^2} \left[ \cos{(\omega_0(t-\tau)) - \cos{(\omega_0 t)}} \right] \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$ Nézzük meg mi történik, ha $\tau \rightarrow 0$. Ez annak felel meg, hogy a rendszer egy pillanatnyi lökést kap, aztán szabadon fejlődik az időben. Egy kis átírással: $$ \underline{q} = \frac{f_0}{m \omega_0^2} \frac{\cos{(\omega_0(t-\tau)) - \cos{(\omega_0 t)}}}{\tau} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$ ami ebben a határesetben nem más lesz, mint egy derivált régimódi képlete. Tehát: $$ \underline{q} \rightarrow \frac{f_0}{m \omega_0} \sin{\omega_0t} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$ a kis löket után a rugók az első módusban rezegnek, azonos irányban. Ennek a frekvenciája $\omega_0$, az amplitúdója pedig $f_0/m\omega_0$.
4.5.3. Baloldali lökés
Mi történik, ha csak az első rugóra hat külső gerjesztés? Ekkor az erő felbontása $$ \underline{F} = \frac{F}{2} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{F}{2} \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$ Ezt kétféleképpen is megkaphatjuk: egyrészt ezt adja a didaktikus szorzatból készített két projektor. Másrészt vegyük észre, hogy ha össze adjuk őket $$ \underline{F} = \frac{F}{2} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{F}{2} \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} = \frac{F}{2}\cdot \begin{pmatrix} 2 \\ 0 \end{pmatrix} $$ akkor csak az első komponensben lesz rezgés, pont ahogyan azt a feladat kéri. Ha nem vagyunk biztosak, akkor csináljuk meg a projektálást.
Minden esetre most az integrálunkban két tag is lesz: $$ \underline{q} = \frac{f_0}{2m\tau} \int_{0}^\tau \frac{\sin{(\omega_1 (t-t^\prime))}}{\omega_1} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{\sin{(\omega_2 (t-t^\prime))}}{\omega_2} \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} \rd t^\prime $$ Ezt kiszámítva $$ \underline{q} = \frac{f_0}{2m\tau \omega_1^2} \left[ \cos{(\omega_1(t-\tau)) - \cos{(\omega_1 t)}} \right] \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{f_0}{2m\tau \omega_2^2} \left[ \cos{(\omega_2(t-\tau)) - \cos{(\omega_2 t)}} \right] \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$ Itt szintén alkalmazzuk a $\tau \rightarrow 0$ határesetet: $$ \underline{q} \rightarrow \frac{f_0}{2m\omega_1} \sin{\omega_1t} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{f_0}{2m\omega_2} \sin{\omega_2 t} \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$ Ez a mozgás tehát két részből áll: azonos irányban feleakkora amplitúdójú rezgést végeznek a rugók mint az első esetben; viszont megjelenik egy ellentétes irányú módus is, a hozzá tartozó $\omega_2$ frekvenciával.
Vegyük még ellenőrzésül radikális esetnek azt, amikor a középső rugón $K=0$, mert ekkor $$\begin{aligned} \omega_0^2 &= \omega_0^2 + 2 \Omega_0^2 \\ \omega_1 &= \omega_2 \end{aligned}$$ Beírva: $$ \underline{q} \rightarrow \frac{f_0}{2m\omega_0} \sin{\omega_0t} \cdot \begin{pmatrix} 1 \\ 1 \end{pmatrix} + \frac{f_0}{2m\omega_0} \sin{\omega_0 t} \cdot \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$ ami kis rendezés után $$ \underline{q} \rightarrow \frac{f_0}{m\omega_0} \sin{\omega_0t} \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$ Aminek örülünk: az első test pontosan úgy mozog, mint a fenti gerjesztő erő esetén; a második pedig nyugalomban marad. Ez logikus, mert $K=0$ mellett nincs rugó ami összekötné a megmozgatott testtel.
4.5.4. Ellentétes szinuszos gerjesztés
Nézzünk meg erre a rendszerre is egy szinuszos gerjesztést $t=0$ kezdettel, ami ellentétesen hat a két testre. Tehát a gerjesztő erőnk: $$ \underline{F}(t) = \Theta(t) f_0 \sin{(\Omega t)} \underline{\eta_2} $$ Erre hattatva a tömegmátrix inverzét: $$ \underline{\underline{M}}^{-1} =\Theta(t) \frac{ f_0}{m} \sin{(\Omega t)} \underline{\eta_2} $$ majd pedig a Green-függvényt, ami most ismét csak az egyik móduson hat: $$ \underline{q} = \int_{-\infty}^\infty \Theta(t-t^\prime) \frac{\sin{(\omega_2 (t-t^\prime))}}{\omega_2} \Theta(t^\prime) \frac{ f_0}{m} \sin{(\Omega t^\prime)} \underline{\eta_2} \rd t^\prime $$ A határok ismét a lépcsőfüggvényekből adódnak: az első miatt a fenti határ $t$, a második miatt a lenti pedig $0$. Tehát: $$ \underline{q} =\frac{f_0}{m \omega_2}\int_{0}^t \sin{(\omega_2 (t-t^\prime))} \sin{(\Omega t^\prime)} \begin{pmatrix} 1 \\ -1 \end{pmatrix} \rd t^\prime $$ Ez az integrál ugyanaz, mint a sima oszcillátornál, szóval a kiszámítását most kihagyjuk. Eredménye: $$ \underline{q} =\frac{f_0}{m \omega_2}\frac{\Omega \sin{\omega_2t} - \omega_2 \sin{\Omega t}}{\Omega^2 - \omega_2^2}\begin{pmatrix} 1 \\ -1 \end{pmatrix} $$
4.6. példa: Egyszerű molekula
Modellezzünk úgy egy kis molekulát, mint 3 test összekötve 2 rugóval. Legyenek a rugók és a kinti tömegek azonosak. Mik lesznek ekkor a sajátmódusok, és hogyan hatnak a rendszerre a külső gerjesztések?

4.6.1. Normálmódusok
Felírva a Lagrange-ot, kis munkával kiderül, hogy itt a mátrixaink: $$\begin{aligned} \underline{\underline{M}} = \begin{pmatrix} m && 0 && 0 \\ 0 && M && 0 \\ 0 && 0 && m \end{pmatrix} \qquad\qquad \underline{\underline{D}} = \begin{pmatrix} k &&- k && 0 \\ -k && 2k && -k \\ 0 && - k && k \end{pmatrix} \end{aligned}$$ Mivel $M$ diagonális, könnyű invertálni: egyszerűen a tömegek reciprokai kellenek egy diagonális mátrixba. A szorzást elvégezve: $$ \underline{\underline{A}} = \omega_0^2 \begin{pmatrix} 1 && -1 && 0 \\ -\frac{m}{M} && 2 \frac{m}{M} && - \frac{m}{M} \\ 0 && -1 && 1 \end{pmatrix} $$ ahol bevezettem megint $\frac{k}{m} = \omega_0^2$-et. Ebből a sajátértékre vonatkozó egyenlet: $$ (\omega_0^2 - \omega^2)^2 \left(2 \omega_0^2 \frac{m}{M} - \omega^2\right) - 2\omega_0^4 \frac{m}{M} (\omega_0^2 - \omega^2) =0 $$
Ránézésre két megoldást is be tudunk tippelni. Legyen az első $\omega = \omega_0$, ami általában egy jó tipp. Az ehhez tartozó sajátvektor $$ \begin{pmatrix} 1-1 && -1 && 0 \\ -\frac{m}{M} && 2 \frac{m}{M}-1 && - \frac{m}{M} \\ 0 && -1 && 1-1 \end{pmatrix} \underline{\eta_0} = 0 $$ alapján olyan lesz, hogy a második komponense nulla; az első és utolsó pedig egymás ellentettjei. Szépen normálva: $$ \underline{\eta_0} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} $$ Amivel meg is van az első módus: ebben a középső atom mozdulatlan, a másik kettő pedig ki-be rezeg körülötte.
A második sajátérték is könnyen tippelhető: legyen $\omega_1 = 0$. Ez is teljesíti az egyenletet, és a hozzá tartozó sajátvektor lehet például: $$ \begin{pmatrix} 1 && -1 && 0 \\ -\frac{m}{M} && 2 \frac{m}{M} && - \frac{m}{M} \\ 0 && -1 && 1 \end{pmatrix} \underline{\eta_1} = 0 $$ $$ \underline{\eta_1} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$ Ez egy nulla frekvenciás rezgés, ami minden koordinátára azonosan hat. Hasonlóan a csúszkáló ingánál látotthoz, ez sem egy rezgés igazából: ez egy eltolás az x tengelyen, ami mindhárom atomra ugyanúgy hat.
A harmadik sajátérték nehezebb: ehhez már egy picit számolni is kell. Tudjuk, hogy ez egyik sajátérték $\omega_0^2$, szóval emeljünk ki a sajátérték egyenletéből $(\omega_0^2 - \omega^2)$-et: $$\begin{aligned} (\omega_0^2 - \omega^2)^2 \left(2 \omega_0^2 \frac{m}{M} - \omega^2\right) - 2\omega_0^4 \frac{m}{M} (\omega_0^2 - \omega^2) =0 \\ (\omega_0^2 - \omega^2) \left[ (\omega_0^2 - \omega^2) \left(2 \omega_0^2 \frac{m}{M} - \omega^2\right) - 2\omega_0^4 \frac{m}{M} \right] = 0 \\ \omega^4 - \omega^2 \omega_0^2\left(1 + 2 \frac{m}{M}\right)+ 2 \omega_0^4 \frac{m}{M} -2\omega_0^4 \frac{m}{M} = 0 \\ \omega^4 - \omega^2 \omega_0^2\left(1 + 2 \frac{m}{M}\right) = 0 \\ \omega^2 \left[\omega^2 -\omega_0^2\left(1 + 2 \frac{m}{M}\right) \right] = 0 \end{aligned}$$ Tehát a harmadik megoldás $\omega_2^2 =\omega_0^2\left(1 + 2 \frac{m}{M}\right) $. Az ehhez tartozó sajátvektor számolását most kihagyom, eredménye: $$ \underline{\eta_2} = \frac{1}{\sqrt{2+4\alpha^2}} \begin{pmatrix} 1 \\ -2 \alpha \\ 1 \end{pmatrix} $$ Ahol $\alpha = \frac{m}{M}$. Ez egy olyan módus, ahol a két szélső azonos irányba mozdul el, a középső viszont ellentétesen. A bejövő tömeges szorzófaktor azért olyan, amilyen, mert a tömegközéppont nem mozdulhat el.
4.6.2. Bal oldali összenyomás
Hattasunk a rendszerre most egy lökés szerű gerjesztőerőt, aminek az alakja: $$\begin{aligned} \underline{F} = F(t) \begin{pmatrix} 2 \\ -2 \\ 0 \end{pmatrix} \qquad\qquad F(t) = \frac{f_0}{\tau}\Theta(t)\Theta(\tau-t) \end{aligned}$$ Tehát a bal oldali és a középső atomokat ellentétes irányba löki, a harmadikat pedig békén hagyja. Erre hattatva a tömegmátrix inverzét: $$ \underline{F} = \underline{\underline{M}}^{-1} \underline{F} = F \begin{pmatrix} 2/m \\ -2/M \\ 0 \end{pmatrix} = \frac{2F}{m} \begin{pmatrix} 1 \\ -\alpha \\ 0 \end{pmatrix} $$
Most nézzük meg tippelés nélkül, hogy hogyan kell ezt felbontani a sajátbázisra. Először is, hálistennek a $\underline{\eta_0}$ és $\underline{\eta_2}$ sajátértékek ortogonálisak, szóval nekik lehetnek a duálisok egyszerűen csak a transzponáltak. Velük: $$\begin{aligned} \underline{\eta_0} \underline{\tilde{\eta_0}} = \frac{1}{2} \begin{pmatrix} 1 && 0 && -1 \\ 0 && 0 && 0 \\ -1 && 0 &&1 \end{pmatrix} \qquad\qquad \underline{\eta_1} \underline{\tilde{\eta_1}} = \frac{1}{2+4\alpha^2}\begin{pmatrix} 1 && -2\alpha && 1 \\ - 2\alpha && 4\alpha^2 && -2\alpha \\ 1 && -2\alpha &&1 \end{pmatrix} \end{aligned}$$ Ezekkel megszorozva a ható erőt: $$\begin{aligned} \underline{\eta_0} \underline{\tilde{\eta_0}}\ \underline{F} =& \frac{F}{m} \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} = \frac{F}{m} \sqrt{2} \underline{\eta_0} \\ \underline{\eta_2} \underline{\tilde{\eta_2}}\ \underline{F} =& \frac{F}{m}\frac{1}{1+2\alpha^2} \begin{pmatrix} 1+2\alpha^2 \\ -2\alpha+4\alpha^2 \\ 1+2\alpha^2 \end{pmatrix} = \frac{F}{m} \sqrt{2+4\alpha^2}\underline{\eta_1} \end{aligned}$$
Ellenőrzésképp láthatjuk, hogy ezeknek az összege tényleg visszaadja $\underline{F}$-et. A harmadik irányra most nincs szükség. Beírva végre a Green-függvényes alakot a rendszer időfejlődésére, az előző példát követve: $$ \underline{q} = \frac{f_0}{m \tau} \int_{0}^t \frac{\sin{(\omega_0 (t-t^\prime))}}{\omega_0} \cdot \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} + \frac{\sin{(\omega_2 (t-t^\prime))}}{\omega_2} \cdot \begin{pmatrix} 1 \\ -2\alpha \\ 1 \end{pmatrix}\rd t^\prime $$ Ezt ismét ki tudjuk integrálni, majd megnézni az érdekes $\tau \rightarrow 0$ határesetet: $$ \underline{q} \rightarrow \frac{f_0}{m} \frac{\sin{(\omega_0 t)}}{\omega_0} \cdot \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} + \frac{f_0}{m} \frac{\sin{(\omega_2 t)}}{\omega_2} \cdot \begin{pmatrix} 1 \\ -2\alpha \\ 1 \end{pmatrix}\rd t^\prime $$ Mivel $\omega_2 = \omega_0 \sqrt{1 + 2 \alpha}$, meg tudjuk nézni mi történik $\alpha = 0$ határesetben: ez azt mondja ki, hogy a középső atom sokkal nehezebb, mint a szélsők. Ekkor a középső test módusai eltűnnek, az mozdulatlan marad. A másik kettőre pedig ebben a határesetben azonos frekvenciájú rezgések hatnak: a jobb oldali testre kioltják egymást, a bal oldalira pedig kétszeres amplitúdójú rezgéseket okoznak.
4.6.3. Eltolás Green-függvénnyel
Azért nézzük még meg az eltoláshoz kapcsolódó módust is, és lássuk be, hogy tényleg az eltolásokhoz kapcsolódik. Legyen a gerjesztőerő $$ \underline{F} = F \begin{pmatrix} 1 \\ \frac{M}{m} \\ 1 \end{pmatrix} $$ amivel $$ \underline{F} = \frac{f}{m} \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$ tehát ő $\underline{\eta_1}$ módushoz tartozik. Ezzel a gerjesztéssel $$ \underline{q} = \frac{f_0}{m \tau} \int_{0}^t \frac{\sin{(\omega_1 (t-t^\prime))}}{\omega_1} \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$
Ne ijedjünk meg, hogy $\omega_1=0$-val osztunk le, helyette számoljunk tovább. Kiintegrálva, majd a szokásos határesetet véve: $$ \underline{q} \rightarrow \frac{f_0}{m} \frac{\sin{(\omega_1 t)}}{\omega_1} \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$ Ezt szorozzuk be eggyel, ami $t/t$: $$ \underline{q} \rightarrow \frac{f_0}{m} \frac{\sin{(\omega_1 t)}}{\omega_1 t} t \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$ Majd használjuk ki, hogy $\frac{\sin{\epsilon}}{\epsilon} \approx 1$, ha $\epsilon$ kicsi. Nekünk most pontosan nulla, szóval elég jó lesz ez a közelítés: $$ \underline{q} \rightarrow \frac{f_0}{m} t \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} $$ Tehát azt kapjuk, hogy mindhárom testet meglökve, azok egy konstans $v = \frac{f_0}{m}$ sebességgel fognak reagálni. Ez egész intuitív, szóval jó látni, hogy végső soron csak ki tud jönni a rezgések nyelvén is.
Teljes duális rendszer
A teljesség jegyében nézzük még meg, hogy hogyan lehetne egy általános irányú gerjesztést is kiszámolni. A bázisunk: $$\begin{aligned} \underline{\eta_0} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ - 1 \end{pmatrix} \qquad\qquad &\underline{\tilde{\eta}_0} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 && 0 && - 1 \end{pmatrix} \\ \underline{\eta_1} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \qquad\qquad &\underline{\tilde{\eta}_1} = ??? \\ \underline{\eta_2} = \frac{1}{\sqrt{2+4\alpha^2}} \begin{pmatrix} 1 \\ -2\alpha \\ 1 \end{pmatrix} \qquad\qquad &\underline{\tilde{\eta}_2} = \frac{1}{\sqrt{2+4\alpha^2}} \begin{pmatrix} 1 && -2\alpha && 1 \end{pmatrix} \end{aligned}$$ Azok a duálisok amik már megvannak jók: rájuk könnyen láthatjuk, hogy teljesül $\underline{\tilde{\eta_i}} \underline{\eta_j} = \delta_{ij}$. Ez $\underline{\eta_1}^T$ transzponálttal nem működne, szóval keressük meg, hogy mivel igen.
Legyen $$ \underline{\tilde{\eta}_1} = \begin{pmatrix} x && y && z \end{pmatrix} $$ majd nézzük meg mindhárom sajátvektorral a skalárszorzatát, és követeljük meg a $\delta$ teljesülését. Ezek rendre három egyenletet adnak: $$\begin{aligned} x + y + z = 1 \\ x - z = 0 \\ x - 2\alpha y + z = 0 \end{aligned}$$ Ezt kicsit átrendezve megoldja: $$\begin{aligned} z &= x \\ x &= \alpha y \\ (2 \alpha + 1 ) y &= 1 \end{aligned}$$ Tehát $$\begin{aligned} x = \frac{ \alpha}{2 \alpha + 1 } \\ y = \frac{1}{2 \alpha + 1 } \\ z = \frac{ \alpha}{2 \alpha + 1 } \\ \end{aligned}$$ Vagy tömörebben $$ \underline{\tilde{\eta_1}} = \frac{1}{2\alpha+1} \begin{pmatrix} \alpha && 1 && \alpha \end{pmatrix} $$
Ezzel a projektorunk $$ \underline{{\eta_1}}\underline{\tilde{\eta_1}} = \frac{1}{2\alpha+1} \begin{pmatrix} \alpha && 1 && \alpha \\ \alpha && 1 && \alpha \\ \alpha && 1 && \alpha \end{pmatrix} $$ Ellenőrzésképp, hogyha ezt hattatjuk a korábbi $$ \underline{F} = \frac{f}{m} \begin{pmatrix} 1 \\ 1 \\1 \end{pmatrix} $$ erőre, akkor eredményül: $$\begin{aligned} \underline{{\eta_1}}\underline{\tilde{\eta_1}}\ \underline{F} &=\frac{f}{m} \frac{1}{2\alpha+1} \begin{pmatrix} \alpha && 1 && \alpha \\ \alpha && 1 && \alpha \\ \alpha && 1 && \alpha \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\1 \end{pmatrix} \\ &= \frac{f}{m} \frac{1}{2\alpha+1} \begin{pmatrix} 2\alpha + 1 \\ 2\alpha + 1 \\ 2\alpha + 1 \end{pmatrix} = \underline{F} \end{aligned}$$ tehát jól dolgoztunk: tényleg ebbe az irányba projektál ez a diadikus szorzat.