Elmecha
6. óra Letöltés
Merev testek
Ha merev testekről beszélünk, az azt jelenti, hogy minden pont közti távolság fix. Ezzel a nagy korlátozással két féle mozgást végezhet a test: vagy minden pontja ugyanarra megy, ez lesz a tömegközépponti mozgás, vagy valahogy forog egy tengely körül. Ezekkel a kinetikus tag: $$ K = \frac{1}{2} M \underline{v}_0^2 + \frac{1}{2} \underline{\omega}\, \underline{\underline{\Theta}} \,\underline{\omega} $$ Ahol $M$ a test össztömege, $\underline{v}_0$ pedig a tömegközéppont sebessége. Emlékeztetőül, a forgási tagban megjelenik a tehetetlenségi nyomaték tenzor: $$ \Theta_{ij} = \int \rd^3 \mathbf{r} \rho(\mathbf{r})\bigl(\delta_{ij}\mathbf{r}^2 - r_i r_j\bigr) $$ ami olyan mint a tömeg, csak a gyorsulásra való tehetetlenség helyett a forgatásra vonatkozik. Ezen felül megjelenik még a forgatás vektoros ábrázolása $\underline{\omega}$-n keresztül: ő mondja meg, hogy milyen tengelyek körül milyen gyorsan forgunk.
Nézzünk először pár példát arra, hogy hogyan kell kiszámolni ezt a tömegszerű mátrixos izét.
6.1. példa: 2+2 tömegpont
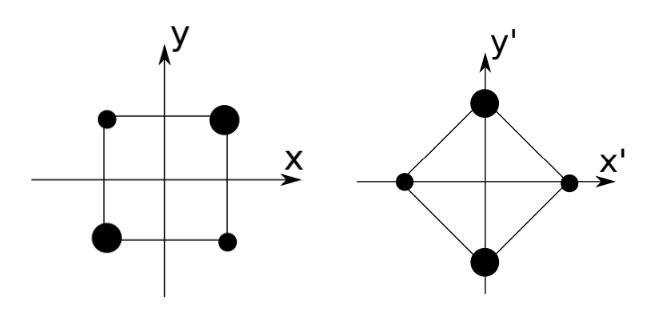
Határozzuk meg ennek a 4-pont-rendszernek a tehetetlenségi tenzorát! Először is: inkább legyünk okosak, és forgassuk el az egészet 45 fokkal, mert úgy egyszerűbb. Nézve a képletet: $$ \begin{aligned} \Theta_{ij} = \int \rd^3 r \rho(\mathbf{r})\bigl(\delta_{ij}r^2 - r_i r_j\bigr) \end{aligned} $$ nekünk itt igazából 4 diszkrét pontunk van: csak szummáznunk kell az egyes pontokra, mert $\rho$ egy pár Dirac delta, ami megeszi az integrálást. $$ \begin{aligned} \Theta_{ij} = \sum_k m_k \bigl(\delta_{ij}r^{k^2} - r_{i}^k r_{j}^k\bigr) \end{aligned} $$ Ezt kiírva például az $xx$ komponensre: $$ \begin{aligned} \Theta_{xx} &= \sum_k m_k \bigl(\delta_{xx}r^{k^2} - r_{x}^k r_{x}^k\bigr) = \sum_k m_k \bigl(r^{k^2} - r_{x}^k r_{x}^k\bigr) \\ &= \sum_k m_k \bigl(x_k^2 + y_k^2 + z_k^2 - x_k^2\bigr) = \sum_k m_k \bigl( y_k^2 + z_k^2\bigr) \end{aligned} $$ A $z$ koordináta mindegyikre nulla. Az $y$ pedig csak a kettő nagy $M$ tömegűre nem: ekkor ha mondjuk $2a$ az oldalhosszúságunk, akkor $y_k = \sqrt{2} a$ $$ \begin{aligned} \Theta_{xx} = M \cdot 2 a^2+ M \cdot 2 a^2= 4 M a^2 \end{aligned} $$ Teljesen hasonlóan: $$ \begin{aligned} \Theta_{yy} = 4 m a^2 \end{aligned} $$
Ami más, az a harmadik irány: $$ \begin{aligned} \Theta_{zz} = \sum_k m_k \bigl(\delta_{zz}r^{k^2} - r_{z}^k r_{z}^k\bigr) = \sum_k m_k \bigl(x^2_k + y^2_k\bigr) \end{aligned} $$ mert ebbe már mind a négy járulékot ad. Beírva: $$ \begin{aligned} \Theta_{zz} = 2\cdot M \cdot (2a^2) + 2\cdot m \cdot (2a^2) = 4 (M+m) a^2 \end{aligned} $$ A vegyes tagok még hátra vannak, mind a három. Ezekből például $$ \begin{aligned} \Theta_{xy} = \sum_k m_k \bigl(\delta_{xy}r^{k^2} - x_k y_k\bigr) = 0 \end{aligned} $$ mert a $\delta$ nulla, illetve nincs olyan tömegpont, amire $x_k \cdot y_k$ ne lenne nulla. A tenzor tehát ebben a forgatott rendszerben: $$ \begin{aligned} \underline{\underline{\Theta}} = 4 a^2\begin{pmatrix} M && 0 && 0 \\ 0 && m && 0 \\ 0 && 0 && M+m \end{pmatrix} \end{aligned} $$
Jó, de minket nem ez érdekelt, hanem ennek a 45 fokkal elforgatott esete. Van már viszont egy mátrixunk: ezt könnyen el tudjuk forgatni egy 3D-s forgásmátrixszal, mivel $$ \begin{aligned} \underline{\underline{\Theta}}^\prime = \underline{\underline{O}}^T \underline{\underline{\Theta}}\ \underline{\underline{O}} \end{aligned} $$ Ez a mátrix most, beírva a szögfüggvényekbe a 45 fokot: $$ \begin{aligned} \underline{\underline{O}} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 && 1 && 0 \\ -1 && 1 && 0 \\ 0 && 0 && \sqrt{2} \end{pmatrix} \end{aligned} $$ A végeredmény egy kis szorozgatás után: $$ \begin{aligned} \underline{\underline{\Theta}}^\prime = 2a^2 \begin{pmatrix} m+M && m-M && 0 \\ m - M && m+M && 0 \\ 0 && 0 && 2(m+M) \end{pmatrix} \end{aligned} $$ Ugyanezt kaptuk volna, ha rögtön ebben a koordinátarendszerben számolunk: csak látszik, hogy $2$ nem nulla tagot kellett volna még figyelembe vennünk.
6.2. példa: Henger
Nézzünk meg egy folytonos tömegeloszlású esetet is. Mi lesz egy homogén henger tehetetlenségi nyomatéka a tömegközéppontra vonatkoztatva? Mivel homogén, így $$ \begin{aligned} \rho(r) = \rho = \text{konst.} \end{aligned} $$ Felírva az integrált: $$ \begin{aligned} \Theta_{ij} = \rho \int \rd^3 r \bigl(\delta_{ij}r^2 - r_i r_j\bigr) \end{aligned} $$ de nekünk csak a henger határaiig kell elmennünk, azokon kívül nincs tömeg. Ehhez térjünk át hengerkoordinátákba, ahol az integrál $$ \begin{aligned} \Theta_{ij} = \rho \int_{-L/2}^{L/2} \rd z \int_0^{2\pi} r \rd \varphi \int_0^R \rd r \bigl(\delta_{ij}q^2 - q_i q_j\bigr) \end{aligned} $$ Itt átírtam az eddig $r$-el jelölt koordinátákat $q$-ra, hogy ne keverjük össze a hengerkoordinátákból a sugárral.
Nézzük meg most a zárójeles kifejezést az egyes komponensekre, és hogy azt hogyan kell kifejezni a koordinátáinkkal. $$ \begin{aligned} ij=zz \qquad\qquad \longrightarrow \qquad\qquad (\delta_{zz}q^2 - q_z q_z\bigr)= x^2 + y^2 = r^2 \end{aligned} $$ ami felülnézetből felrajzolva a problémát vizuálisan is látszik. Tehát erre a komponensre: $$ \begin{aligned} \Theta_{zz} &= \rho \int_{-L/2}^{L/2} \rd z \int_0^{2\pi} \rd \varphi \int_0^R \rd r\ r^3 \\ &= \rho L \int_0^{2\pi} \rd \varphi \int_0^R \rd r\ r^3 \\ &= 2\pi \rho L \int_0^R \rd r\ r^3 \\ &= 2\pi \rho L \frac{R^4}{4} = R^2 \pi L \frac{R^2}{2} \\ &= \frac{M}{2} R^2 \end{aligned} $$ A másik kettőre: $$ \begin{aligned} ij=yy \qquad\qquad \longrightarrow \qquad\qquad (\delta_{yy}q^2 - q_y q_y\bigr)= x^2 + z^2 = r^2 \sin^2{\varphi} + z^2 \end{aligned} $$ Na ez már bonyolultabb: $$ \begin{aligned} \Theta_{yy} &= \rho \int_{-L/2}^{L/2} \rd z \int_0^{2\pi} \rd \varphi \int_0^R \rd r\ r( r^2\sin^2{\varphi} + z^2) \\ &= \rho \int_{-L/2}^{L/2} \rd z \int_0^{2\pi} \rd \varphi \ ( \frac{R^4}{4}\sin^2{\varphi} + \frac{R^2}{2} z^2) \\ &= \rho \int_0^{2\pi} \rd \varphi \ ( L \frac{R^4}{4}\sin^2{\varphi} + \frac{L^3}{3\cdot 4}\frac{R^2}{2} ) \\ &= \rho ( L \frac{R^4}{4} \pi + \frac{L^3}{3\cdot 4}\frac{R^2}{2} 2 \pi) \\ &= \frac{M}{12} (L^2 + 3 R^2) \end{aligned} $$ De szerencsére ugyanez lesz $xx$-re is. Minden más tagban pedig olyanok jelennek meg, hogy $$ \begin{aligned} \int_0^{2\pi} \sin{\varphi}\cos{\varphi} \propto \int_0^{2\pi} \sin{2\varphi}, && \int_0^{2\pi} \sin{\varphi}, && \int_0^{2\pi} \cos{\varphi} \end{aligned} $$ Amik mint teljes periódusra integrálnak sima szögfüggvényeket: ezeket felrajzolva beláthatjuk, hogy nullát adnak.
Tehát a tehetetlenségi tenzorunk: $$ \begin{aligned} \underline{\underline{\Theta}} = \frac{M}{12} \begin{pmatrix} L^2 + 3R^2 && 0 && 0 \\ 0 && L^2 + 3R^2 && 0 \\ 0 && 0 && 6 R^2 \end{pmatrix} \end{aligned} $$ Egy fontos részt leolvashatunk ennek jobb alsó sarkából: ha körbe forog egy hengerünk, a tehetetlenség nem függ a $z$ irányú hosszától, nagysága pedig $\frac{1}{2} M R^2$. A henger felülnézetből pedig nem más mint egy korong, így: $$ \begin{aligned} \Theta_{korong} = \frac{1}{2} M R^2 \end{aligned} $$ Egy másik érdekes határeset, amikor a henger sokkal hosszabb, mint szélesebb. Ezt köznyelven rúdnak hívjuk, matematikailag pedig $L\gg R$-nek, amit beírva a tenzorba megkapjuk a rúd középpontja körüli forgatásokra vonatkoztatott tehetetlenségét: $$ \begin{aligned} \Theta_{rúd}^{CM} = \frac{1}{12} M L^2 \end{aligned} $$ Ha esetleg az érdekel minket, hogy egy rúd a középpontja helyett az egyik vége körül mennyire ellenáll a forgatásokra, azt a párhuzamos tengelyek (Steiner) tétele alapján kapjuk: $$ \begin{aligned} \Theta_{rúd}^{vég} = \Theta^{CM} + M d^2 = \frac{L^2}{3} M \end{aligned} $$ Ha a jövőben szükség lenne rá, akkor ennek a tételnek a mátrixos alakja $$ \begin{aligned} \underline{\underline{\Theta}} = \underline{\underline{\Theta}}^{CM} + M \left(\delta_{ij} \underline{d}^2 - d_i d_j\right) \end{aligned} $$
6.3. példa: Tömeges Atwood gép
Vegyünk egy egyszerű Atwood gépet, $m$ és $M$ tömegekkel. Viszont most vegyük figyelembe, hogy a csiga is forog: az $\mu$ tömegű, és $R$ sugarú. Mik lesznek ekkor a mozgásegyenletek?
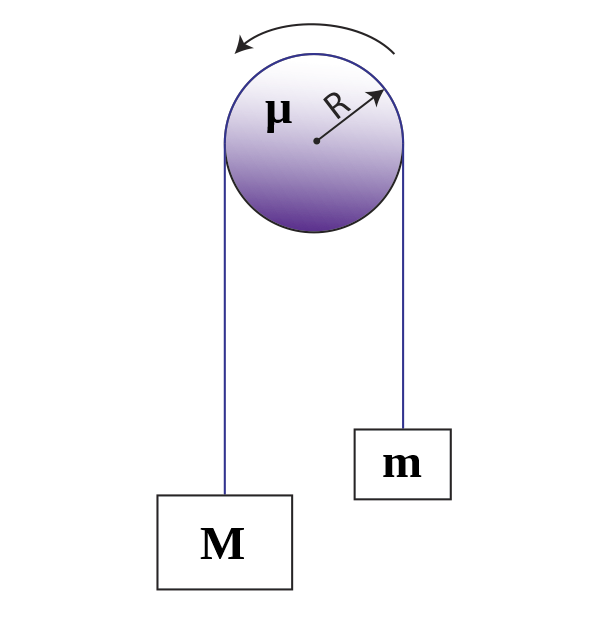
A teljesen általános Lagrange-unk ezúttal: $$ \begin{aligned} \mathcal{L} = \frac{1}{2} m \dot{y}_1^2 + \frac{1}{2} M \dot{y}_2^2 + m g y_1 + M g y_2 + \frac{1}{2} \Theta \omega^2 \end{aligned} $$ Kiróhatunk viszont pár kényszert: mivel a kötél hossza fix, így $$ \begin{aligned} y_2 = - y_1 \end{aligned} $$ Vagy másképp kifejezve, a kötél minden pontja azonos sebességgel mozog, mert különben szétcsúszna: $$ \begin{aligned} |\dot{y_1}| = |\dot{y_2}| = |\dot{y}| \end{aligned} $$ A kötél pedig nem csúszhat el a csigán: tehát $$ \begin{aligned} \dot{y} = R \omega \end{aligned} $$
Beírva még az előző feladatból a nyomatékot, a Lagrange-unk végső alakja: $$ \begin{aligned} \mathcal{L} = \frac{1}{2} \dot{y}^2 (m+M) + g (m-M)y + \frac{1}{4} \mu \dot{y}^2 \end{aligned} $$ Ebből az Euler Lagrange eredménye: $$ \begin{aligned} \ddot{y} \left[(m+M) + \frac{1}{2} \mu \right] = g (m-M) \end{aligned} $$ Legyen most $M = 2m $, $\mu = m$, amikkel $$ \begin{aligned} \ddot{y} \left[3m + \frac{1}{2} m \right] &= - g m \\ \ddot{y} &= \frac{2}{7} g \end{aligned} $$ egy konstans gyorsulást tapasztalunk.
6.4. példa: Forgatott rúd
Vegyünk egy $m$ tömegű, $l$ hosszúságú rudat, rögzítsük az egyik végét a plafonhoz úgy, hogy forogni tudjon, de másképp elmozdulni ne. Kezdjük el forgatni valamilyen állandó $\omega$ szögsebességgel a felfüggesztési pontjától lehúzott vertikális tengely körül. Mi lesz a rúd vízszintessel bezárt szöge?
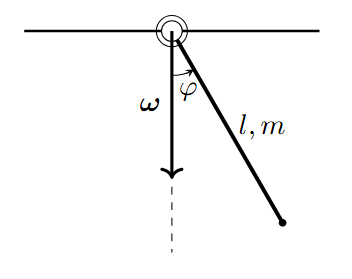
Kis emlékeztetőként $$ \begin{aligned} \Theta = \frac{1}{3} m l^2 \end{aligned} $$ a tehetetlenség, a rúd végére merőleges forgatásokra. Itt a forgatás lefelé mutat: annak a rúdra merőleges komponense $$ \begin{aligned} \omega_\perp = \omega \sin{\varphi} \end{aligned} $$ ami a rúd végére vonatkoztatott forgatásoknak feleltethető meg. Itt hangsúlyoznám, hogy $\omega_\perp$ vektora nem keverendő össze a rá ható erővel. Ez egy axiálvektor, a forgatás mit ő ír le jobbkéz-szabály szerint adódik, és itt a képernyő felől az olvasó irányába mutat. Ha szépen szeretnénk kiszámolni a feladatot, akkor tenzorosan és vektorosan kellene felírni a problémát, amiből ugyanaz fog kijönni.
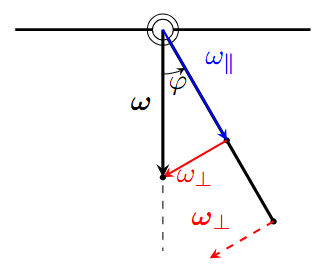
A potenciális tagunkban vehetjük a teljes tömeget a rúd közepébe, így $$ \begin{aligned} V = - m g \frac{l}{2} \cos{\varphi} \end{aligned} $$ Tehát a Lagrange most: $$ \begin{aligned} \mathcal{L} &= \frac{1}{2} \Theta \omega_\perp^2 + \frac{1}{2}m g l \cos{\varphi} \\ &= \frac{1}{2} \frac{1}{3} m l^2 \omega^2 \sin^2{\varphi} + \frac{1}{2}m g l \cos{\varphi} \end{aligned} $$ Erre ráküldve egy Euler-Lagrange-ot: $$ \begin{aligned} 0 = - \frac{1}{2}mgl \sin{\varphi} + \frac{2}{6} m l^2 \omega^2 \sin{\varphi} \cos{\varphi} \end{aligned} $$ lesz a mozgásegyenlet.
Ennek egy lehetséges megoldása $$ \begin{aligned} \sin{\varphi} = 0 \qquad\qquad \longrightarrow \qquad\qquad \varphi = 0 \end{aligned} $$ Ami teljesen logikus: azt írja le, hogy a rúd egyenesen lefelé lóg. Ezt letudva leoszthatunk vele, így $$ \begin{aligned} g&= \frac{2}{6} l \omega^2 \cos{\varphi} \\ \cos{\varphi} &= \frac{3}{2}\frac{g}{l} \frac{1}{\omega^2} \end{aligned} $$ Nevezzük el megszokásból a dolgokat: $$ \begin{aligned} \cos{\varphi} = \frac{3}{2} \frac{\omega_0^2}{\omega^2} \end{aligned} $$ Na de ez korlátos, $-1 \leq \cos{} \leq 1$: csak akkor lesz ez a megoldás valid, ha $$ \begin{aligned} \frac{3}{2} \frac{\omega_0^2}{\omega^2} &\leq 1 \\ \frac{3}{2} \omega_0^2 &\leq \omega^2 \end{aligned} $$ Minden más esetben csak a 0 kitérés lesz opció. A megoldás tehát úgy néz ki, hogy a forgatás sebességét növelve egyszer csak elkezd a rúd kilengeni. Végtelen gyors forgatás esetén pedig derékszöget tapasztalunk.