Elmecha
7. óra Letöltés
Hamiltoni mechanika
A Lagrange-i mechanikával már nagyon jól megbarátkoztunk. Ennek lényege tömören hogy egy $\mathcal{L}(q, \dot{q},t)$ Lagrange-függvényből az E-L egyenletek segítségével megkapjuk a mozgásegyenletet valamilyen $\ddot{q} = f(q, \dot{q})$ alakban. Ez egy szép, relatíve könnyen követhető lépésekből álló folyamat eredménye, ami miatt hasznos és szemléletes.
Viszont a másodrendű diffegyenleteket nem szeretjük annyira, mint az elsőrendűeket. Sokkal kezelhetőbb, ha ehelyett átírjuk a mozgásegyenletet kétszer annyi elsőrendű diffegyenletté. Ez a Hamiltoni mechanika egyik előnye. A másik az, hogy a kvantummechanika is ezen a nyelven íródott, szóval nem árt megbarátkozni vele klasszikusan is.
Hogy áttérjünk a Lagrange-i formalizmusból a Hamiltoniba, néhány egyszerű lépést kell csak tennünk. Lagrange-függvény helyett most Hamilton-unk lesz: $$ \begin{aligned} \mathcal{H}(\underline{q},\underline{p}) = \underline{p}^T\ \dot{\underline{q}}(\underline{p}) -\mathcal{L}(\underline{q}, \dot{\underline{q}}(\underline{p})) \end{aligned} $$ aminek a változói a(z általános) koordináta és az (általános) impulzus.
Az Euler-Lagrange egyenlet helyett most két darab Hamilton egyenletünk lesz, amikből megkapjuk a két elsőrendű diffegyenletet: $$ \begin{aligned} \dot{\underline{q}} = \frac{\partial \mathcal{H}}{\partial \underline{p}} \qquad\qquad \dot{\underline{p}} = -\frac{\partial \mathcal{H}}{\partial \underline{q}} \end{aligned} $$ A negatív előjel itt fontos, ne felejtsük el. Ha emlékezni akarunk rá, akkor idézzük vissza hogy $\dot{p} = F = - \nabla V$.
7.1. példa: Egyszerű rugó
Nézzünk meg először egy egyszerű példát: egy sima, egy dimenziós rugót. Ennek a Lagrange-függvénye ugyebár $$ \begin{aligned} \mathcal{L} = K - V = \frac{1}{2} m \dot{x}^2 - \frac{1}{2} k x^2 \end{aligned} $$ Hogy áttérjünk a Hamiltoni formalizmusra, először is kell valami jó $p$ impulzusváltozó. Ez lehet a már korábbról ismert általános impulzus: $$ \begin{aligned} p = \frac{\partial \mathcal{L}}{\partial \dot{x}} = m \dot{x} \end{aligned} $$ Tehát az egyenleteinkben $\dot{x} = \frac{p}{m}$ lesz, így a Lagrange az általános koordinátával ($q=x$) és impulzussal kifejezve: $$ \begin{aligned} \mathcal{L}(q,\dot{q}(p)) = \frac{1}{2} m \left( \frac{p}{m}\right)^2 - \frac{1}{2} k q^2 = \frac{1}{2m} p^2 - \frac{1}{2} k q^2 \end{aligned} $$
Beírva ezt, és $p\dot{q}$-t a Hamiltoni definíciójába: $$ \begin{aligned} \mathcal{H}(q,p) &= p \frac{p}{m} - \frac{1}{2m} p^2 + \frac{1}{2} k q^2 \\ \mathcal{H}(q,p) &= \frac{1}{2m} p^2 + \frac{1}{2} k q^2 \end{aligned} $$ Ha szemfülesek vagyunk, akkor feltűnhet, hogy ez pont a rendszer teljes $E=K+V$ energiája. Ez gyakran így van, de nem mindig. Részletes tárgyalást a Goldsteinben találunk, de nagyjából: ha konzervatív a potenciál, illetve nem függ a sebességektől, továbbá az általános koordináták kényszerei időfüggetlenek, akkor $\mathcal{H} = E$. Nekünk ez a legtöbb feladatban teljesül, de később még visszatérünk rá egy kis általánosítással.
Mik lesznek ekkor a mozgásegyenletek? Egy-egy deriválás után: $$ \begin{aligned} \dot{q} = \frac{\partial \mathcal{H}}{\partial p} = \frac{p}{m} \qquad\qquad -\dot{p} = \frac{\partial \mathcal{H}}{\partial q} = k q \end{aligned} $$ Tehát $$ \begin{aligned} \dot{q} = \frac{1}{m} p \qquad\qquad\dot{p} = - k q \end{aligned} $$ Amit fel is írhatunk mátrixosan, kis gyakorlásként: $$ \begin{aligned} \frac{\rd}{\rd t}\begin{pmatrix} q \\ p \end{pmatrix} = \begin{pmatrix} 0 && 1/m\\ -\omega^2 && 0 \end{pmatrix} \begin{pmatrix} q \\ p \end{pmatrix} \end{aligned} $$ Ahol $\omega^2 = \frac{k}{m}$. Ennek a feladatnak a megoldását persze már ismerjük: deriváljuk le még egyszer az egyik Hamilton egyenletet. $$ \begin{aligned} \ddot{q} = \frac{1}{m} \dot{p} = - \omega^2 q \end{aligned} $$
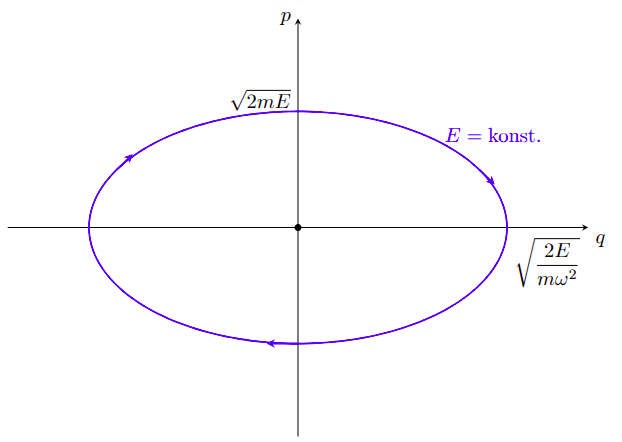
Ezt már párszor megoldottuk: $$ \begin{aligned} q(t) &= A \cos{(\omega t + \varphi)} \\ \dot{q}(t) &= - \omega A\sin{(\omega t + \varphi)} \end{aligned} $$ amit visszaírva megvan az impulzus is: $$ \begin{aligned} p(t) = - m\omega A\sin{(\omega t + \varphi)} \end{aligned} $$ Ezt is fel lehet írni vektorosan: $$ \begin{aligned} \begin{pmatrix} q \\ p \end{pmatrix}(t) = A \begin{pmatrix} \cos{(\omega t + \varphi)} \\ - m\omega \sin{(\omega t + \varphi)} \end{pmatrix} \end{aligned} $$ Kicsit nézegetve ezt szét tudjuk kapni pár részre: $$ \begin{aligned} \begin{pmatrix} q \\ p \end{pmatrix}(t) = A \begin{pmatrix} 1 && 0 \\ 0 && - m\omega \end{pmatrix} \begin{pmatrix} \cos{(\omega t + \varphi)} \\ \sin{(\omega t + \varphi)} \end{pmatrix} \end{aligned} $$ Rajzoljuk le ennek a mozgásnak a fázisterét! Ehhez képzeljünk el egy olyan koordinátarendszert, aminek egyik tengelye $q$, a másik pedig $p$. Rakjuk le a tollunkat valamilyen kezdeti pontban, ami megfelel a $t=0$ pillanatnak, aztán ahogy telik az idő, kövessük le egy görbével azt, hogy melyik pontokba halad tovább a rendszer. Ez a trajektória, amit a rendszerünk a mozgás során bejár.
A fenti példánkra ez relatíve egyszerű: van jobb oldalt egy körünk. Ez meg van szorozva egy nyújtást (és tükrözést) végző mátrixxal, meg valami irreleváns konstanssal. Tehát a fázistér nem lesz más, mint egy ellipszis. Gyakran szokás az $A$ szabad paramétert lecserélni valamire, ami a kezdeti feltételekből adott. Ez lehet például az energia: itt például ha a $t=0$ pillanatban $p=0$ és $\varphi = 0$ akkor $$ \begin{aligned} E = 0+\frac{1}{2} m \omega^2 A^2 \cos^2{(\omega t + \varphi)} = \frac{1}{2} m \omega^2 A^2 \\ A = \pm\sqrt{\frac{2E}{m \omega^2}} \end{aligned} $$ Tehát az ellipszis szélei konstans energia mellett: $$ \begin{aligned} p\Big|_{q=0} = \mp m\omega \sqrt{\frac{2E}{m \omega^2}} = \mp \sqrt{2mE} \\ q\Big|_{p=0} = \pm\sqrt{\frac{2E}{m \omega^2}} \end{aligned} $$ Az pedig, hogy merre mutat az áramlás most fizikai intuícióból adódik. Ha jobbra ($+$) van kitérítve a testünk, akkor onnan balra ($-$) fog gyorsulva visszarugózni. Tehát ha $q$ pozitívból megy a negatív felé, akkor $p$ negatív. Fordítva is igaz: ha a jobb oldali szélső pont felé halad a testünk, de még nincs ott, akkor pozitív lendülete lesz.
7.2. példa: Csillapított oszcillátor
Nézzük meg ehhez képest, hogy mi lesz a csillapított oszcillátor mozgásegyenlete. Az ő Lagrange-a: $$ \begin{aligned} \mathcal{L} = \left(\frac{1}{2} m \dot{x}^2 -\frac{1}{2}m\omega^2 x^2 \right)e^{\gamma t} \end{aligned} $$ szép explicit időfüggést tartalmaz. De nem baj, attól még tudunk számolni, például egy kanonikus impulzust: $$ \begin{aligned} p = m \dot{x} e^{\gamma t} \qquad\qquad \dot{x} = \frac{1}{m} e^{-\gamma t} p \end{aligned} $$ Szóval $$ \begin{aligned} p \dot{x}(p) &= \frac{1}{m} e^{-\gamma t} p^2 \\ \mathcal{L}(x, \dot{x}(p)) &= \frac{1}{2m} p^2 e^{-\gamma t} - \frac{1}{2}m\omega^2 x^2 e^{\gamma t} \end{aligned} $$
Összerakva: $$ \begin{aligned} \mathcal{H}(x,p) = \frac{1}{2m} p^2 e^{-\gamma t} + \frac{1}{2}m\omega^2 x^2 e^{\gamma t} \end{aligned} $$ ami nem a mechanikából szokásos energia. Annak az alakja $E_m =\frac{1}{2}m \dot{x}^2 + V$, szóval kis matekkal $\mathcal{H} =E_m e^{\gamma t}$. Minden esetre a mozgásegyenletek még igazak: $$ \begin{aligned} \dot{x} = \frac{1}{m} p e^{-\gamma t} \qquad\qquad \dot{p} = - m\omega^2 x e^{\gamma t} \end{aligned} $$ Mit tudunk mondani ezeknek a megoldásáról? Nézzük meg először, hogy van-e fixpontja az egyenleteknek: $$ \begin{aligned} 0 = \frac{1}{m} p e^{-\gamma t} \rightarrow p = 0 \\ 0 = - m\omega^2 x e^{\gamma t} \rightarrow x = 0 \end{aligned} $$
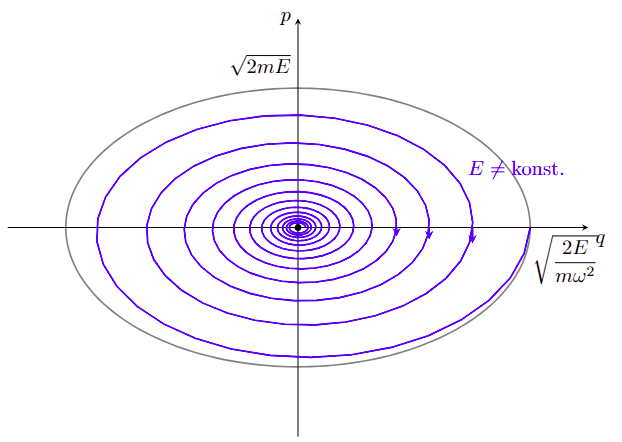
Van, méghozzá az origó. Kis mellébeszéléssel nézzük meg, stabil-e. Térítsük ki az egyensúlyi pontból a rendszert egy kis $\Delta x$ és $\Delta p$ távolsággal. Ekkor: $$ \begin{aligned} \dot{x} = \frac{1}{m} e^{-\gamma t} \Delta p \qquad\qquad \dot{p} = - m\omega^2 e^{\gamma t} \Delta x \end{aligned} $$ Ha kellően sok idő eltelt, akkor $e^{-\gamma t} \approx 0$, tehát az elsőt elhanyagolhatjuk. A második előjele pont ellentétes a kitérítés irányával: ez a pont egy stabil vonzópont lesz. A fázistéren ezt fel tudjuk rajzolni a sima oszcillátor alapján, csak egy különbséggel: a trajektóriák az origóba tartanak, miután $t>0$. Attól függően, hogy túlcsillapított-e az oszcillátorunk; vagy keringenek körülötte párat, vagy rögtön belezuhannak.
Érdeklődőknek:
Igazából ez egy jó nagy mellébeszélés, aminek szinte semmi igazságalapja nincs. Valójában a stabilitásvizsgálatot itt célszerűbb $q-\dot{q}$ térben elvégezni, mert ott kiderül, hogy ez egy vonzó fixpont, mert a fixpontban kiértékelt Jacobi sajátértékeinek valós része mindig negatív. A képzetes részeik pedig megadják a mozgás oszcilláló mivoltját: ha eltűnnek, túlcsillapítást tapasztalunk.
7.3. példa: Potenciálvölgyek
Nézzünk egy (talán már ismerős) egy dimenziós rendszert, amelynek potenciális energiája $$ \begin{aligned} V=A(q^2-v^2)^2 \end{aligned} $$ ahol $v$ valamilyen konstans. Ekkor a Hamilton $$ \begin{aligned} \mathcal{H}(q,p) = \frac{p^2}{2m} + A(q^2-v^2)^2 \end{aligned} $$ A belőle fakadó egyenletek: $$ \begin{aligned} \dot{q} &= \frac{\partial \mathcal{H}}{\partial p} = \frac{p}{m} \\ \dot{p} &= -\frac{\partial \mathcal{H}}{\partial q} =-4Aq(q^2-v^2) \end{aligned} $$ Milyen fixpontjai vannak ezeknek? $$ \begin{aligned} p_0 &= 0 \\ q_0 = 0 \qquad \qquad &\text{vagy} \qquad \qquad q_0 = \pm v \end{aligned} $$
Fixpontból három fajta lehet:
- Vonzó, ami bevonzza a trajektóriákat. Ide tarthat a rendszer végtelen idő után.
- Taszító, ami taszítja a trajektóriákat. Itt nagyon nem akar lenni a rendszer.
- Nyeregpont, ami egyes irányokban vonz, másik irányokban pedig taszít.
Ezután ki kell számítani a fixpontban vett mátrix $\lambda$ sajátértékeit:
- Ha $\forall \mathcal{R}e(\lambda)>0$, akkor taszító.
- Ha $\forall \mathcal{R}e(\lambda)<0$, akkor vonzó.
- Ha is-is, akkor nyeregpont.
- Illetve ha $\mathcal{I}m(\lambda)$≠$0$, akkor oszcilláló mozgást fogunk tapasztalni.
Most nézzük meg ezeknek a stabilitását rendesen! Ehhez szükségünk van a Jacobi mátrixra, amely definíció szerint $$ \begin{aligned} \frac{\rd}{\rd t} \begin{pmatrix} q \\ p \end{pmatrix} = \underline{f}(q,p) \\ \underline{\underline{J}} = \begin{pmatrix} \partial_q f_1 && \partial_p f_1 \\ \partial_q f_2 && \partial_p f_2 \end{pmatrix} \end{aligned} $$ tehát esetünkben $$ \begin{aligned} \underline{\underline{J}} = \begin{pmatrix} 0 && 1/m\\ -4A(q^2-v^2) -8Aq^2 && 0 \end{pmatrix} \end{aligned} $$ Őt kell kiértékelni a fixpontokban, majd kiszámolni a sajátértékeit. Először is $q_0=v$ esetén $$ \begin{aligned} \underline{\underline{J}}\Big|_{q_0=v} = &\begin{pmatrix} 0 && 1/m\\ -8Av^2 && 0 \end{pmatrix} \\ &\lambda_\pm = \pm i \sqrt{\frac{8A}{m}} v \end{aligned} $$ ezek képzetesek. Róluk több mindent nem tudunk mondani a lineáris stabilitásvizsgálattal: az annyiban merül ki, hogy valami oszcilláló keringésre számítunk körülöttük.
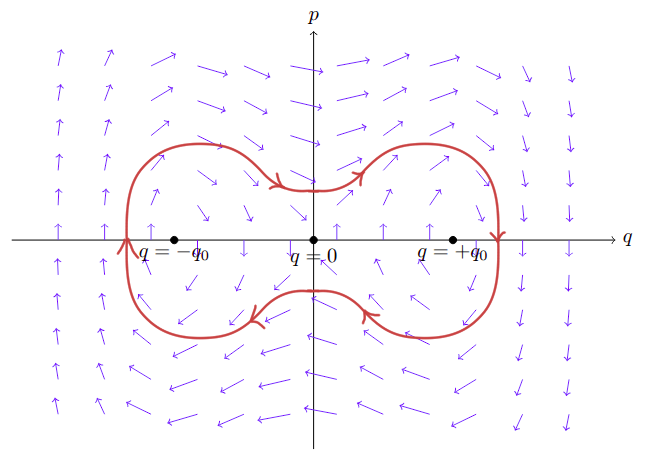
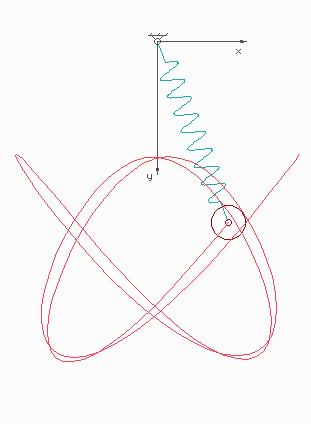
Másrészt $$ \begin{aligned} \underline{\underline{J}}\Big|_{q_0=0} = &\begin{pmatrix} 0 && 1/m\\ 4Av^2 && 0 \end{pmatrix} \\ &\lambda_\pm = \pm \sqrt{\frac{4A}{m}} v \end{aligned} $$ amik valósak: az egyik pozitív, a másik negatív. Ez azt jelenti, hogy ő egy nyeregpont lesz: az egyik irányból bevonzza, a másikban pedig kitaszítja a trajektóriákat. Meg tudjuk nézni még a sajátvektorait is: $$ \begin{aligned} \underline{u}_+ \propto \begin{pmatrix} 1\\ v\sqrt{4Am} \end{pmatrix} \qquad \qquad \underline{u}_- \propto \begin{pmatrix} 1\\ -v\sqrt{4Am} \end{pmatrix} \end{aligned} $$ Amikről azt látjuk, hogy a taszítóhoz tartozó egy pozitív meredekségű egyenes irányába mutat, a másik, vonzó irány pedig rá merőleges. Ezt össze tudjuk vetni a lenti, gép által generált ábrával:
7.4. példa: Rugós inga
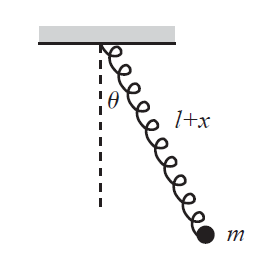
Véve egy $l$ nyugalmi hosszúságú rugót, és azt felfüggesztve egy plafonra, a Lagrange-unk: $$ \begin{aligned} \mathcal{L}(\underline{q}, \dot{\underline{q}}) = \frac{1}{2} m \dot{r}^2 + \frac{1}{2} m (l+r)^2 \dot{\varphi}^2 + mg(l+r) \cos{\varphi} - \frac{1}{2} m \omega^2 r^2 \end{aligned} $$ Hogy áttérjünk a Hamiltoni formalizmusra, kellenek először is a kanonikus impulzusok, amikből most kettő is lesz: $$ \begin{aligned} p_r = \frac{\partial \mathcal{L}}{\partial \dot{r}} = m \dot{r} \qquad\qquad p_\varphi = \frac{\partial \mathcal{L}}{\partial \dot{\varphi}} = m (l+r)^2 \dot{\varphi} \end{aligned} $$ Illetve ezeknek az invertálása, hogy ki tudjuk fejezni a sebességeket az impulzusokkal: $$ \begin{aligned} \dot{r} = \frac{1}{m} p_r \qquad\qquad \dot{\varphi} = \frac{1}{m(l+r)^2} p_\varphi \end{aligned} $$ Tehát a Hamiltonhoz kellő tagok: $$ \begin{aligned} \underline{p}^T\underline{\dot{q}}(\underline{p}) &= \frac{1}{m} p_r^2 + \frac{1}{m(l+r)^2} p_\varphi^2 \\ \mathcal{L}(\underline{q}, \dot{\underline{q}}(\underline{q}, \underline{p})) &= \frac{1}{2 m } p_r^2 + \frac{1}{2m(l+r)^2} p_\varphi^2 + mg(l+r) \cos{\varphi} - \frac{1}{2} m \omega^2 r^2 \end{aligned} $$
Összekombinálva, a Hamilton: $$ \begin{aligned} \mathcal{H} &= \frac{1}{m} p_r^2 + \frac{1}{m(l+r)^2} p_\varphi^2 - \frac{1}{2 m } p_r^2 - \frac{1}{2m(l+r)^2} p_\varphi^2 - mg(l+r) \cos{\varphi} + \frac{1}{2} m \omega^2 r^2 \\ &= \frac{1}{2 m } p_r^2 + \frac{1}{2m(l+r)^2} p_\varphi^2 - mg(l+r) \cos{\varphi}+ \frac{1}{2} m \omega^2 r^2 \end{aligned} $$ Ebből a mozgásegyenleteket egy-egy deriválással kapjuk: $$ \begin{aligned} \dot{r} &= \frac{\partial \mathcal{H}}{\partial p_r} = \frac{1}{m} p_r \qquad &\dot{\varphi} = \frac{\partial \mathcal{H}}{\partial p_\varphi} = \frac{1}{m} \frac{1}{(l+r)^2} p_\varphi \\ - \dot{p_r} &= \frac{\partial \mathcal{H}}{\partial r} = -\frac{1}{m} \frac{1}{(l+r)^3} p_\varphi^2 - mg \cos{\varphi} + m \omega^2 r \qquad &- \dot{p_\varphi} = \frac{\partial \mathcal{H}}{\partial \varphi} = mg(l+r)\sin{\varphi} \end{aligned} $$ Megkaptuk a négy differenciálegyenletet, ami leírja a mozgást. Hogy valamit ránézésre is tudjunk róla mondani, nézzük meg, hogy van-e egyensúlyi pontja ezeknek, illetve ha igen, akkor hol. Egyensúly akkor van, ha a fenti egyenletek mindegyike nulla, tehát: $$ \begin{aligned} 0 &= \frac{1}{m} p_r \qquad &0 = \frac{1}{m} \frac{1}{(l+r)^2} p_\varphi \\ 0 &= -\frac{1}{m} \frac{1}{(l+r)^3} p_\varphi^2 - mg \cos{\varphi} + m \omega^2 r \qquad &0 = mg(l+r)\sin{\varphi} \end{aligned} $$ Ezek szerint $$ \begin{aligned} p_r &=0 && p_\varphi = 0 \\ 0 &= -\frac{1}{m} \frac{1}{(l+r)^3} p_\varphi^2 - mg \cos{\varphi} + m \omega^2 r && \varphi = n\pi \end{aligned} $$
Innen az utolsó előtti a legbonyolultabb. Beleírva a többit ($\cos{n\pi} = \pm 1$, $p_\varphi=0$), azt látjuk, hogy $$ \begin{aligned} 0 &= \mp mg + m \omega^2 r \\ \pm g &= \omega^2 r \\ \frac{g}{r} &= \pm \omega^2 \end{aligned} $$ Két ilyen pont lesz tehát: az egyik lent $\varphi=0$ irányban, a másik pedig fent ahol $\varphi=\pi$ (most tegyük fel, hogy nincs fal felette, vagy mágikusan át tud rajta haladni). Mindkét esetben a rugó ingaszerű megnyúlása ($g/L$-es jellemző frekvenciája) kapcsolatban lesz a rugó saját frekvenciájával, egyedül az iránya az ami eltér. Fent egy picit összenyomódik, lent pedig egy picit megnyúlik.
7.5. példa: Kisrezgések
Erre nem nézünk meg specifikus példát, mert a következő az állítás: itt is ugyanúgy lehet kisrezgéseket vizsgálni mátrixosan. A rezgéses Lagrange általános esetben: $$ \begin{aligned} \mathcal{L} = \frac{1}{2} \underline{\dot{q}}^T \underline{\underline{M}}\, \underline{\dot{q}} - \frac{1}{2} \underline{q}^T \underline{\underline{D}}\, \underline{q} \end{aligned} $$ Amiből kellenek nekünk a kanonikus impulzusok. Egy szimbolikus deriválással $$ \begin{aligned} \underline{p} = \underline{\underline{M}}\, \underline{\dot{q}} \qquad\qquad \underline{p}^T = \underline{\dot{q}}^T \underline{\underline{M}} \end{aligned} $$ Amit invertálnunk kell, hogy megkapjuk a sebességeket az impulzusokkal kifejezve: $$ \begin{aligned} \underline{\underline{M}}^{-1}\underline{p} = \underline{\dot{q}} \qquad\qquad \underline{p}^T \underline{\underline{M}}^{-1} = \underline{\dot{q}}^T \end{aligned} $$
Beírva a Lagrange-ba: $$ \begin{aligned} \mathcal{L}(\underline{q},\underline{\dot{q}}(\underline{p})) &= \frac{1}{2} \underline{p}^T \underline{\underline{M}}^{-1} \underline{\underline{M}} \underline{\underline{M}}^{-1}\underline{p} - \frac{1}{2} \underline{q}^T \underline{\underline{D}} \underline{q} \\ \mathcal{L}(\underline{q},\underline{\dot{q}}(\underline{p})) &= \frac{1}{2} \underline{p}^T \underline{\underline{M}}^{-1}\underline{p} - \frac{1}{2} \underline{q}^T \underline{\underline{D}} \underline{q} \end{aligned} $$ Ehhez jön még hozzá $$ \begin{aligned} \underline{\dot{q}}^T \underline{p} = \underline{p}^T \underline{\underline{M}}^{-1} \underline{p} \end{aligned} $$ Amiket beírva: $$ \begin{aligned} \mathcal{H} = \frac{1}{2} \underline{p}^T \underline{\underline{M}}^{-1}\underline{p} + \frac{1}{2} \underline{q}^T \underline{\underline{D}}\, \underline{q} \end{aligned} $$ Ebből a Hamilton egyenletek egyszerűen deriválással kijönnek: $$ \begin{aligned} \underline{\dot{q}} = \underline{\underline{M}}^{-1}\underline{p} \qquad\qquad \underline{\dot{p}} = - \underline{\underline{D}}\, \underline{q} \end{aligned} $$ Deriválva mégegyszer az elsőt (feltéve hogy $\underline{\underline{M}}^{-1}$ konstans, mint például egy kisrezgés esetén), és behelyettesítve a másodikat: $$ \begin{aligned} \underline{\ddot{q}} &= \underline{\underline{M}}^{-1} \underline{\dot{p}} \\ &=- \underline{\underline{M}}^{-1} \underline{\underline{D}}\, \underline{q} \end{aligned} $$ egy ismerős egyenletet kapunk: innentől megint jöhetnek a normálmódusok, pont ahogy eddig.
Ami viszont hasznos még akkor is, ha nem rezgésekre vagyunk kíváncsiak, az a Hamiltonra való áttérés mátrixos útja. Ha felírható ilyen mátrixos alakban a Lagrange (tehát négyzetesen szerepelnek a sebességek benne, és "szépen" keverednek) akkor elég felírnunk a tömegmátrixot, és invertálnunk. Például a fenti rugós ingára $$ \begin{aligned} \underline{\underline{M}} &= m\begin{pmatrix} 1 && 0 \\ 0 &&(l+r)^2 \end{pmatrix} \\ \underline{\underline{M}}^{-1} &= \frac{m}{m^2(l+r)^2}\begin{pmatrix} (l+r)^2 && 0 \\ 0 &&1 \end{pmatrix} = \frac{1}{m(l+r)^2}\begin{pmatrix} (l+r)^2 && 0 \\ 0 &&1 \end{pmatrix}\\ K(\underline{q},\underline{p}) &= \frac{1}{2} \underline{p}^T\, \underline{\underline{M}}^{-1}\underline{p} = \frac{p_r^2}{2m} + \frac{p_\varphi^2}{2m(l+r)^2} \end{aligned} $$ Ez meg tud spórolni nekünk pár deriválást, ha például egy sok dimenziós rendszerről beszélünk. Azért a biztonság kedvéért érdemes a deriválgatással számolnunk még, főleg ha nem vagyunk biztosak benne, hogy "szép"-e a Lagrange eléggé.