Elmecha
8. óra Letöltés
Poisson zárójelek
Barátkozzunk kicsit a Poisson-zárójelekkel! Definíció szerint: $$ \begin{aligned} \{f,g\} = \partial_qf \partial_p g - \partial_p f \partial_q g \end{aligned} $$ ami jó, mert velük le lehet írni egy tetszőleges bárminek az időfejlődését: $$ \begin{aligned} \frac{\rd}{\rd t} f = \{f, \mathcal{H}\} + \partial_t f \end{aligned} $$ Különös szerepük van még a Hamiltoni mechanikában a kanonikus változók Poisson-zárójeleinek is.
Definíció szerint, $q$ és $p$ akkor kanonikusak, ha: $$ \begin{aligned} \{q_i, q_j\} &= \frac{\partial q_i}{\partial q_l} \frac{\partial q_j}{\partial p_l} - \frac{\partial q_i}{\partial p_l} \frac{\partial q_j}{\partial q_l} \\ &= 0 \end{aligned} $$ hasonlóképp $$ \begin{aligned} \{p_i, p_j\} &= \frac{\partial p_i}{\partial q_l} \frac{\partial p_j}{\partial p_l} - \frac{\partial p_i}{\partial p_l} \frac{\partial p_j}{\partial q_l} \\ &= 0 \end{aligned} $$ illetve $$ \begin{aligned} \{q_i, p_j\} &= \frac{\partial q_i}{\partial q_l} \frac{\partial p_j}{\partial p_l} - \frac{\partial q_i}{\partial p_l} \frac{\partial p_j}{\partial q_l} \\ &= \delta_{il} \delta_{jl} - 0 \\ &= \delta_{ij} \end{aligned} $$
8.1. példa: Perdület
Számoljunk ki valami bonyolultabbat is, például a perdületek Poisson-zárójelét: $$ \begin{aligned} \{L_i, L_j\} = ? \end{aligned} $$ ahol $$ \begin{aligned} L_i = \epsilon_{ijk} x_j p_k \end{aligned} $$ Beírva: $$ \begin{aligned} \{L_i, L_j\} = \frac{\partial L_i}{\partial q_l} \frac{\partial L_j}{\partial p_l} - \frac{\partial L_i}{\partial p_l} \frac{\partial L_j}{\partial q_l} \end{aligned} $$ Például az első: $$ \begin{aligned} \frac{\partial L_i}{\partial q_l} = \frac{\partial \epsilon_{ijk} q_j p_k}{\partial q_l} = \epsilon_{ijk}p_k \frac{\partial q_j}{\partial q_l} = \epsilon_{ijk}p_k \delta_{jl} = \epsilon_{ilk}p_k \end{aligned} $$ Teljesen hasonlóan a többi is: $$ \begin{aligned} \frac{\partial L_j}{\partial p_l} = \frac{\partial \epsilon_{jmn} q_m p_n}{\partial p_l} = \epsilon_{jmn} q_m \frac{\partial p_n}{\partial p_l} = \epsilon_{jml} q_m \end{aligned} $$ Szóval összegezve: $$ \begin{aligned} \{L_i, L_j\} &= (\epsilon_{ilk}p_k)(\epsilon_{jml} q_m) - (\epsilon_{ipl} q_p)(\epsilon_{jln} p_n) \\ &= \epsilon_{ilk}\epsilon_{jml} p_k q_m - \epsilon_{ipl}\epsilon_{jln}q_p p_n \end{aligned} $$
Használjuk ki, hogy $$ \begin{aligned} \epsilon_{oab}\epsilon_{oxy} = \delta_{ax}\delta_{by} - \delta_{ay}\delta_{bx} \end{aligned} $$ Meg permutáljunk párat ciklikusan, amivel $$ \begin{aligned} \epsilon_{ilk}\epsilon_{jml} p_k q_m &= \epsilon_{lik}\epsilon_{ljm} p_k q_m \\ &= \delta_{ij}\delta_{km} p_k q_m - \delta_{im}\delta_{jk} p_k q_m \\ &= \delta_{ij} p_k q_k - p_j q_i \end{aligned} $$ Illetve a másikra: $$ \begin{aligned} \epsilon_{ipl}\epsilon_{jln}q_p p_n &= \epsilon_{lip}\epsilon_{ljn}q_p p_n \\ &= \delta_{ij}\delta_{pn}q_p p_n - \delta_{in}\delta_{pj}q_p p_n \\ &= \delta_{ij} q_p p_p - q_j p_i \end{aligned} $$ Ebben van egy összegzett index: az nyugodtan átírható, mondjuk $k$-ra. Ezzel a teljes: $$ \begin{aligned} \{L_i, L_j\} &= \delta_{ij} p_k q_k - p_j q_i - \delta_{ij} p_k q_k +q_j p_i \\ &= q_j p_i - p_j q_i \\ &= (\delta_{jn} \delta_{im} - \delta_{jm} \delta_{in} ) q_n p_m \\ &= \epsilon_{oji} \epsilon_{onm} q_n p_m \\ &= \epsilon_{oji} (\epsilon_{onm} q_n p_m) \\ &= \epsilon_{oji} L_o \end{aligned} $$ Tehát: $$ \begin{aligned} \{L_i, L_j\} = \epsilon_{kji} L_k \end{aligned} $$ ami egy egészen nevezetes eredmény, jegyezzük meg.
Kanonikus transzformációk
Előadáson beláttuk, hogy a Hamiltont nem csak egy fázistéren lehet vizsgálni: át tudunk térni másik koordinátákra, amelyekre szintén validak lesznek a Hamilton egyenletek; feltéve, hogy ez a transzformáció kanonikus. Mikor kanonikus egy trafó a $q,p$ fázistérből a $Q,P$ fázistérre? Akkor, ha $$ \begin{aligned} \{Q_i, P_j\}_{q,p} = &\ \delta_{ij} = \{q_i,p_j\}_{Q,P} \\ \{Q_i, Q_j\}_{q,p} = \{P_i,P_j\}_{q,p} = &\ 0 = \{q_i, q_j\}_{Q,P} = \{p_i,p_j\}_{Q,P} \end{aligned} $$ Tehát ha az új koordinátáknak a régiekben vett Poisson zárójelei kanonikusak. Az, hogy melyik a régi és melyik az új, az nem számít.
Ez nagyon hasznos tud lenni arra, hogy egy bonyolultnak tűnő feladatot átírjunk valami egyszerűbbé. Nézzünk erre is egy példát!
8.2. példa: Egy csúnya(?) Hamilton
Nézzünk meg egy bonyolult Hamiltont, sejtsünk meg rá egy kanonikusnak vélt trafót, aztán bizonyítsuk be, hogy tényleg az is. Legyen a kalapból kihúzott Hamiltonunk: $$ \begin{aligned} \mathcal{H} = \frac{1}{2a} \ln{P^{Q^{2}}}\ln{P^{P^{2}}} - \frac{1}{2}a \omega^2 \left( \left(QP\right)^i +\left(QP\right)^{-i}\right) \end{aligned} $$ Ezt még alakítsuk kicsit. Tudjuk a logaritmikus azonosságokból, hogy $$ \begin{aligned} \ln{P^{Q^{2}}} = Q^{2} \ln{P} \end{aligned} $$ Illetve $$ \begin{aligned} \cos{x} &= \frac{e^{ix} + e^{-ix}}{2} \\ \cos{\ln{x}} &= \frac{e^{i\ln{x}} + e^{-i\ln{x}}}{2} = \frac{x^i + x^{-i}}{2} \end{aligned} $$ Amivel $$ \begin{aligned} \cos{\ln{QP}} = \frac{(QP)^i + (QP)^{-i}}{2} \end{aligned} $$ Tehát a Hamilton $$ \begin{aligned} \mathcal{H} = \frac{1}{2a} Q^2 P^2 \ln^2{P} - a \omega^2 \cos{\ln{(QP)}} \end{aligned} $$
Egy másik kalapból kihúzva, szép lenne a Hamilton, ha $$ \begin{aligned} p = QP \ln{P} \qquad\qquad q = \ln{(QP)} = \ln{Q} + \ln{P} \end{aligned} $$ Kanonikus-e ez a transzformáció? Nézzük meg: $$ \begin{aligned} \{q,p\}_{Q,P} &= \frac{1}{Q} \cdot Q\left( \ln{P} + \frac{P}{P}\right) - \frac{1}{P} \cdot P \ln{P} \\ &=\ln{P} + 1 - \ln{P} = 1 \end{aligned} $$ Ez teljesül. A másik kettő triviális, de azért kiírva: $$ \begin{aligned} \{q,q\}_{Q,P} &= \frac{1}{Q} \frac{1}{P} - \frac{1}{Q} \frac{1}{P} = 0 \\ \{p,p\}_{Q,P} &= P \ln{P} \cdot Q (\ln{P}+1) - P \ln{P} \cdot Q (\ln{P}+1) = 0 \end{aligned} $$ Tehát a Hamilton az úgy rendszerben, szintén kanonikus változókkal: $$ \begin{aligned} \mathcal{H} &= \frac{p^2}{2a} - a\omega^2 \cos{q} \\ &= \frac{p^2}{2mR^2} - mgR \cos{Q} \end{aligned} $$ ami egy ismerős rendszert ír le: az egyszerű ingát.
Teljes rendszervizgálat
Ezen módszerek birtokában szinte már bármit meg tudunk mondani. Nézzünk most egy részletes példát, amiben összefoglalunk nagyjából mindent ami kellhet egy tipikus feladat megoldásához.
8.3. példa: Minden egy helyen
8.3.1. Kanonikus transzformációk
Vegyünk egy képzelt rendszert, amely Hamilton függvénye: $$ \begin{aligned} \mathcal{H} = \frac{P^2 }{2m \sin^2{Q}} e^{-\gamma t} + a(\sin{\cos{Q}})^2 e^{\gamma t} \end{aligned} $$ szeretnénk ezt megoldani, de ránézésre nem tűnik túl egyszerűnek vagy szépnek. Ilyenkor mindig megpróbálkozhatunk (sokféleképpen) egy kanonikus transzformáció segítségével szebb alakra hozni a Hamiltont. Azt, hogy hogyan tudjuk szebbé transzformálni ízlés kérdés: itt a fizikai intuícióra ™ kell hivatkoznunk.
Például ennél a rendszernél: én szeretném, hogy a kinetikus tagunkban csak a kanonikus impulzus jelenjen meg. Szóval hasraütésre legyen $$ \begin{aligned} p = \frac{P}{\sin{Q}} \end{aligned} $$ Ami majd kiderül, hogy nem teljesen jó, de azt is jó megtanulni, hogy hogyan lehet korrigálni.Ezen felül a $\sin{\cos{Q}}$ se túl szép: legyen $$ \begin{aligned} \cos{Q} = q \qquad \longrightarrow \qquad Q = \arccos{q} \end{aligned} $$ amivel $$ \begin{aligned} P = p \sin{\arccos{q}} = p \sqrt{1 - q^2} \end{aligned} $$
Vajon ez kanonikus transzformáció-e? Nézzük meg a Poisson-zárójelek segítségével: $$ \begin{aligned} \{Q, P\}_{q,p} &= \frac{\partial Q}{\partial q}\frac{\partial P}{\partial p} - \frac{\partial Q}{\partial p}\frac{\partial P}{\partial q} \\ &= - \frac{1}{\sqrt{1 - q^2}} \sqrt{1 - q^2} - 0 \\ &= -1 \end{aligned} $$ Ez pont egy előjellel tér el attól amit szeretnénk. Módosítsuk a változóinkat úgy, hogy ez magjavuljon: legyen például $$ \begin{aligned} p = -\frac{P}{\sin{Q}} \end{aligned} $$ amivel már jók vagyunk. Ezen felül meg illik még nézni a másik két zárójelet is: $$ \begin{aligned} \{Q, Q\}_{q,p} &= \frac{\partial Q}{\partial q}\frac{\partial Q}{\partial p} - \frac{\partial Q}{\partial p}\frac{\partial Q}{\partial q} \\ &= 0-0=0 \end{aligned} $$ illetve az egy fokkal bonyolultabb: $$ \begin{aligned} \{P, P\}_{q,p} &= \frac{\partial P}{\partial q}\frac{\partial P}{\partial p} - \frac{\partial P}{\partial p}\frac{\partial P}{\partial q} \\ &= -\frac{pq}{\sqrt{1-q^2}} \sqrt{1 - q^2} + \sqrt{1 - q^2} \frac{pq}{\sqrt{1-q^2}} = 0 \end{aligned} $$ Ez most még triviális volt, de nem baj, ha gyakorlunk arra az esetre, amikor nem lesz az (több dimenziós esetben). Minden esetre beláttuk, hogy ezzel a változócserével is kanonikusak maradunk: érvényesek rájuk is a Hamilton egyenletek.
8.3.2. Hamilton egyenletek
Kihasználva a fentieket, a trafó után a Hamiltonunk: $$ \begin{aligned} \mathcal{H} = \frac{p^2}{2m} e^{-\gamma t} + a\sin^2{q}\ e^{\gamma t} \end{aligned} $$ A feladat kedvéért most csalok egy kicsit: az előző koordináták alapján $q$ csak $\pm1$ közé eshetne. Most demonstrációs célokkal legyen $q \in [-\pi, \pi]$. Ezzel a megkötéssel tudjuk ábrázolni a potenciális energia exponenciális lecsengés nélküli részét:
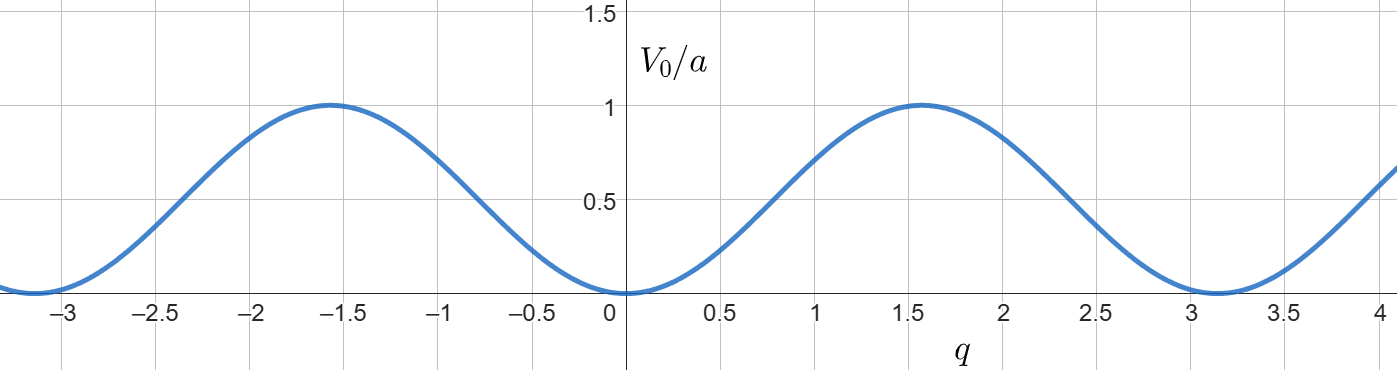
Mit tudunk mondani a mozgásról? Ehhez először is érdemes felírnunk a mozgásegyenleteket: $$ \begin{aligned} \dot{q} &= \frac{\partial \mathcal{H}}{\partial p} \qquad\qquad \ \ \, \dot{p} = - \frac{\partial \mathcal{H}}{\partial p} \\ m \dot{q} &= p\ e^{-\gamma t} \qquad\qquad \dot{p} = - 2 a \sin{q} \cos{q}\ e^{\gamma t} \end{aligned} $$ Megoldani őket természetesen már más tészta: numerikusan biztos lehetséges. Analitikusan és vizuálisan viszont anélkül is tudunk mondani valamit, a fázisterek és a fixpontvizsgálat módszereinek használatával.
8.3.3. Fázistér
A fázistér felrajzolásához kelleni fog, hogy milyen kezdeti energiával indult a rendszer. Legyen ez most $$ \begin{aligned} \mathcal{H}(t=0) = \frac{p^2}{2m} + a \sin^2{q} = a \end{aligned} $$ Mivel egy disszipatív rendszerünk van, az energia ennél csak kisebb lesz: a fázisterünk határai tehát $$ \begin{aligned} \frac{p^2}{2m} + a \sin^2{q} &\leq a \\ \frac{p^2}{2m} &\leq a - a \sin^2{q} = a\cos^2{q} \\ p^2 &\leq 2ma\cos^2{q} \\ |p| &\leq \sqrt{2ma} |\cos{q}| \end{aligned} $$
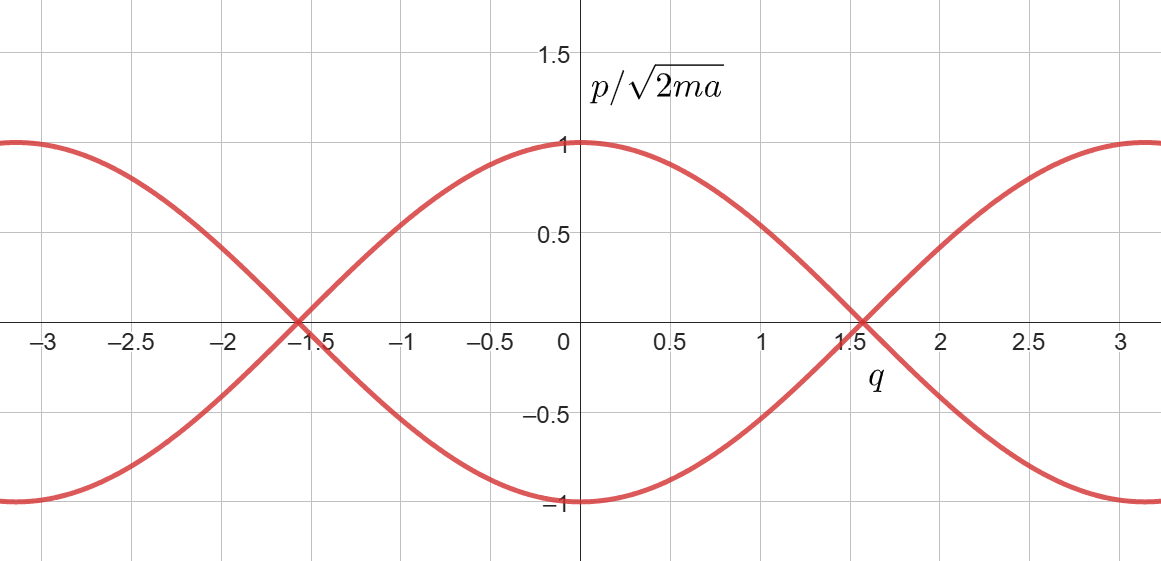
8.3.4. Fixpontvizsgálat
Van nekünk egy egyenletrendszerünk, mégpedig $$ \begin{aligned} \dot{q} &= \frac{p}{m} \ e^{-\gamma t} \\ \dot{p} &= - 2 \sin{q} \cos{q}\ e^{\gamma t} \end{aligned} $$ Az első relatívve könnyű kérdés amit fel tudunk tenni: van-e ezeknek egy olyan pontja, amibe ha a rendszer belekerül (akár mert odarakjuk, akár magától) akkor ott is marad? Ezek a $(q_0, p_0)$ fixpontok, amiket úgy kapunk, hogy a fenti egyenleteket nullává tesszük: $$ \begin{aligned} 0 &= \frac{p_0}{m} \ e^{-\gamma t} \\ 0 &= - 2 \sin{q_0} \cos{q_0}\ e^{\gamma t} \end{aligned} $$ Ennek megoldásai: $$ \begin{aligned} p_0 &= 0 \\ q_0 &\in \{0, \pm \frac{\pi}{2}, \pm \pi\} \end{aligned} $$
A fixpontok bekategorizálása megy például a lineáris stabilitásvizsgálattal. Csináljuk ezt meg most a mi egyenleteinkre! Először is, a Jacobi: $$ \begin{aligned} \underline{\underline{J}} = \begin{pmatrix} 0 && \frac{e^{-\gamma t}}{m} \\ -2e^{\gamma t}(\cos^2{q}-\sin^2{q}) && 0 \end{pmatrix} \end{aligned} $$ Vegyük ezt most a $p=0$, $q=\pi /2$ pontban! Ott $\sin^2{\frac{\pi}{2}} = 1$, $\cos^2{\frac{\pi}{2}} = 0$, tehát a Jacobi: $$ \begin{aligned} \underline{\underline{J}}|_{\pi/2} = \begin{pmatrix} 0 && \frac{e^{-\gamma t}}{m} \\ 2e^{\gamma t} && 0 \end{pmatrix} \end{aligned} $$ Ennek a sajátértékei: $$ \begin{aligned} \lambda^2 = 2e^{\gamma t}\frac{e^{-\gamma t}}{m} = \frac{2}{m} \end{aligned} $$ Az egyik pozitív, a másik negatív: ez tehát egy nyeregpont lesz.
Nézzük meg ugyanezt a $0,\pm \pi$ pontokban. Ott $$ \begin{aligned} \underline{\underline{J}}|_{\pi/2} = \begin{pmatrix} 0 && \frac{e^{-\gamma t}}{m} \\ -2e^{\gamma t} && 0 \end{pmatrix} \end{aligned} $$ aminek a sajátértékei $$ \begin{aligned} \lambda^2 = -\frac{2}{m} \end{aligned} $$ tisztán képzetesek. Na erről nem mondott semmit a lineáris stabilitásvizsgálat: nem is fog. Itt kivételesen tudunk viszont trükközni egyet: a Hamiltoni mechanikánkból térjünk vissza a jó öreg Lagrange-ira: $$ \begin{aligned} m \ddot{q} &= \dot{p} e^{-\gamma t} - \gamma p e^{-\gamma t} \\ m \ddot{q} &= -2 \sin{q}\cos{q} - \gamma p e^{-\gamma t} \end{aligned} $$ És visszadézve a csillapított oszcillátort: $$ \begin{aligned} p = \frac{\partial \mathcal{L}}{\partial \dot{q}} = m \dot{q} e^{\gamma t} \end{aligned} $$ tehát $$ \begin{aligned} m \ddot{q} = -2 \sin{q}\cos{q} - \gamma m \dot{q} \end{aligned} $$ Nevezzük el $\dot{q}$-t mondjuk $z$-nek! Ekkor $$ \begin{aligned} \dot{q} &= z \\ m\dot{z} &= -2 \sin{q} \cos{q} - \gamma m z \end{aligned} $$
Erre ugyanúgy rá tudjuk küldeni a fixpontvizsgálatot. A Jacobi itt: $$ \begin{aligned} \underline{\underline{J}} = \begin{pmatrix} 0 && 1 \\ -\frac{2}{m}(\cos^2{q}-\sin^2{q}) && -\gamma \end{pmatrix} \end{aligned} $$ Amit már nullában (illetve $\pm \pi$-ben) kiértékelve kicsit mást kapunk: $$ \begin{aligned} -&\lambda(-\gamma -\lambda) + \frac{2}{m} = 0 \\ &\lambda^2 + \gamma \lambda + \frac{2}{m} = 0 \\ &\lambda_\pm = -\frac{\gamma}{2} \pm \frac{1}{2}\sqrt{\gamma^2 - \frac{8}{m}} \end{aligned} $$ Bárhogy nézzük, $\sqrt{\gamma^2 - \frac{8}{m}}$ kisebb lesz gammánál: még a plusszos megoldás esetében sem tudja pozitívvá tenni a sajátértéket. Tehát mindkettő negatív: ezek a pontok vonzópontok lesznek. Mindezeknek a tudatában fel tudjuk rajzolni a fázisteret, és ránézésre megmondani, hogy egy tetszőleges kezdeti feltételekből indított ponttal nagyjából mi fog történni.
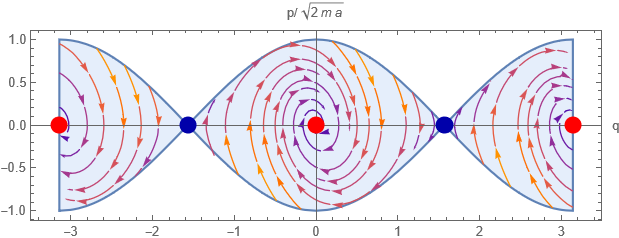
8.3.5. Időfüggő mennyiségek
Kíváncsiak lehetünk rá, hogy ebben a rendszerben hogyan változnak a koordinátákon kívül egyéb dolgok is. Nézzük meg például, hogy hogyan változik a kinetikus tag az időben: $$ \begin{aligned} \dot{K} = \{K, \mathcal{H}\} + \partial_t K \end{aligned} $$ ahol $$ \begin{aligned} K = \frac{p^2}{2m} e^{-\gamma t} \end{aligned} $$ Számoljuk ki a parciális deriváltját: $$ \begin{aligned} \partial_t K =- \gamma \frac{p^2}{2m} e^{-\gamma t} = - \gamma K \end{aligned} $$ illetve a Poisson zárójelét: $$ \begin{aligned} \{K, \mathcal{H}\} &= \frac{\partial K}{\partial q}\frac{\partial \mathcal{H}}{\partial p} - \frac{\partial K}{\partial p}\frac{\partial \mathcal{H}}{\partial q} = \\ &=0\frac{\partial \mathcal{K}}{\partial p} - \frac{\partial K}{\partial p}\frac{\partial V}{\partial q} = \\ & = - \frac{p}{m} e^{-\gamma t} \cdot 2a \sin{q} \cos{q} e^{\gamma t} \\ &= - \frac{2a}{m} p \sin{q} \cos{q} \end{aligned} $$
Hasonlóképp, a potenciális tagra: $$ \begin{aligned} \partial_t V = \gamma V \end{aligned} $$ $$ \begin{aligned} \{V, \mathcal{H}\} &= \frac{\partial V}{\partial q}\frac{\partial \mathcal{H}}{\partial p} - \frac{\partial V}{\partial p}\frac{\partial \mathcal{H}}{\partial q} \\ &= \frac{\partial V}{\partial q}\frac{\partial K}{\partial p} -0 \\ &= \frac{2a}{m} p \sin{q} \cos{q} \end{aligned} $$ Kicsit átírva a dolgokat $$ \begin{aligned} K &= \frac{p^2}{2m}e^{-\gamma t} \ \ \, \qquad \longrightarrow \qquad p = \sqrt{2mK} e^{\gamma t/2}\\ V &= a \sin^2{q} e^{\gamma t} \qquad \longrightarrow \qquad \sin{q} = \sqrt{\frac{V}{a}}e^{-\gamma t/2} \end{aligned} $$ Az utóbbiból jön még, hogy $$ \begin{aligned} \sin{q} &= \sqrt{\frac{V}{a}}e^{-\gamma t/2} \\ \sin^2{q} &= \frac{V}{a}e^{-\gamma t} \\ \cos^2{q} &= 1 - \frac{V}{a}e^{-\gamma t} \\ \cos{q} &= \sqrt{e^{\gamma t} - \frac{V}{a}}e^{-\gamma t/2} \end{aligned} $$ Ezeket beírva: $$ \begin{aligned} \dot{K} &= - \frac{2a}{m} \sqrt{2mK} e^{\gamma t/2} \sqrt{\frac{V}{a}}e^{-\gamma t/2} \sqrt{1 - \frac{V}{a}}e^{-\gamma t/2} - \gamma K \\ \dot{K} &= - 2 \sqrt{2\frac{a}{m}KV\left(e^{\gamma t} - \frac{V}{a} \right)}e^{-\gamma t/2} - \gamma K \\ \dot{V} &= 2 \sqrt{2\frac{a}{m}KV\left(e^{\gamma t} - \frac{V}{a} \right)}e^{-\gamma t/2} + \gamma V \end{aligned} $$
Ami szintén egy teljesen valid diffegyenlet-rendszer. Érdekes lehet még ehelyett az energiák $E$ összegét és $\Delta$ különbségét is vizsgálni: $$ \begin{aligned} \dot{E} &=\frac{\rd}{\rd t}(K+V) = -\gamma (K-V) \\ \dot{\Delta} &=\frac{\rd}{\rd t}(K-V) = - 4 \sqrt{2\frac{a}{m}KV\left(e^{\gamma t} - \frac{V}{a} \right)}e^{-\gamma t/2} - \gamma (K+V) \end{aligned} $$ Kellően sok idő után ez közelítőleg $$ \begin{aligned} \dot{E} &= -\gamma \Delta \\ \dot{\Delta}& = - \gamma E \end{aligned} $$ tehát $$ \begin{aligned} \ddot{E} = \gamma^2 E \qquad\qquad \ddot{\Delta} = \gamma^2 \Delta \end{aligned} $$ mind az összenergia, mind a kinetikus és potenciális energiák különbsége exponenciálisan lecseng. Legalábbis ez lenne, ha nem hibáztam volna a feladatban pár sorral korábban. Ettől függetlenül szép az eredménye, szóval itthagyom. Ha $a$ pici, akkor még közelítőleg valid is.
8.3.6. Periódusidő
Legyen most $\gamma = 0$! Tehát $$ \begin{aligned} \mathcal{H} = \frac{p^2}{2m} + a \sin^2{q} \end{aligned} $$ Ilyenkor csak keringés van: mennyi a frekvenciája? Ehhez nézzünk egy új koordináta trafót: $$ \begin{aligned} J = \oint_{E=E_0} p \rd q && P = \frac{1}{2\pi }\oint_{E=E_0} p \rd q \end{aligned} $$ amit egy olyan körintegrállal definiálunk, ahol konstans az energia. A $2\pi$ itt konvenció: előadáson lemaradt, picit más lesz a jelentése $J$-nek és $P$-nek (nem szokás amúgy őket megkülönböztetni így betűkkel de az első a hatás a második pedig a redukált hatás). Legyen a $t=0$ pillanatban ez a konsans energia valami $E$ szám.
Ekkor, ha megmarad: $$ \begin{aligned} E =\frac{p^2}{2m} + a \sin^2{q} \end{aligned} $$ ami jó, mert a fenti integrálba ki kell fejeznünk $$ \begin{aligned} E &=\frac{p^2}{2m} + a \sin^2{q} \\ E&-a \sin^2{q} = \frac{p^2}{2m} \\ p &= \pm \sqrt{2m(E-a \sin^2{q})} \end{aligned} $$ most az élet egyszerűsítése végett legyen $$ \begin{aligned} E(t=0) = a \end{aligned} $$ amivel $$ \begin{aligned} p_\pm &= \pm \sqrt{2mE\cos^2{q}} \\ p_\pm &= \pm \sqrt{2mE}\ |\cos{q}| \end{aligned} $$
Az integrálhoz rajzoljuk fel, hogy hogyan néz ki egy periódus: először legurulunk a lejtőn, aztán fel a másik oldalt, aztán pedig vissza ugyanúgy. Tehát a $q$ koordinátánkban elindulunk $-\frac{\pi}{2}$-től, elmegyünk $\frac{\pi}{2}$-ig, aztán vissza. Mindez alatt milyen az impulzus iránya? Amíg meg nem fordulunk a második dombtetőn addig pozitív, utána viszont negatív. Tehát az integrálunk, és az ő határai határai: $$ \begin{aligned} J &= \oint_{E=E_0} p \rd q \\ &= \int_{-\pi/2}^{\pi/2} p_+ \rd q + \int_{\pi}^{-\pi} p_- \rd q \\ &= \int_{-\pi/2}^{\pi/2} p_+ \rd q - \int_{-\pi}^{\pi} p_- \rd q \\ &= \int_{-\pi/2}^{\pi/2} p_+ \rd q + \int_{-\pi}^{\pi} p_+ \rd q \\ &= 2 \int_{-\pi/2}^{\pi/2} p_+ \rd q \end{aligned} $$ Ezt már csak el kell végezni. Amit kapunk: $$ \begin{aligned} J = 2\sqrt{2mE} \underbrace{\int_{-\pi/2}^{\pi/2} |\cos{q}| \rd q}_{=2} = 4\sqrt{2mE} \end{aligned} $$ egy konstans, ami egy jó impulzus változó: a kérdés az, hogy mi lesz a hozzá tartozó $Q$ ciklikus koordináta.
Tegyük fel, hogy kanonikusak. Ekkor $$ \begin{aligned} \dot{Q} = \frac{\partial \mathcal{H}}{\partial J} = \nu(J) \end{aligned} $$ Mi nekünk $J$, és vele a Hamilton? $$ \begin{aligned} J &= 4\sqrt{2mE} \\ J^2 &= 32 m E \\ E &= \frac{1}{32 m}J^2 \end{aligned} $$ tehát $$ \begin{aligned} \dot{Q} = \nu(J) = \frac{\partial E}{\partial J} = \frac{J}{16 m} = \frac{1}{4 m}\sqrt{2mE} = \frac{1}{4}\sqrt{\frac{2E}{m}} \end{aligned} $$ Ez lesz tehát a körmozgás $\nu$ frekvenciája. Vele a periódusidő egyszerűen $$ \begin{aligned} T = \frac{1}{\nu} = 4\sqrt{\frac{m}{2E}} \end{aligned} $$